Next: Ideles and Ideals Up: Global Fields and Adeles Previous: The Adele Ring Contents Index
The proof of Lemma 20.4.1 below will use in a crucial way
the normalized Haar measure on ![]() and the induced measure on the
compact quotient
and the induced measure on the
compact quotient
![]() . Since I am not formally developing
Haar measure on locally compact groups, and since I didn't explain
induced measures on quotients well in the last chapter, hopefully the
following discussion will help clarify what is going on.
. Since I am not formally developing
Haar measure on locally compact groups, and since I didn't explain
induced measures on quotients well in the last chapter, hopefully the
following discussion will help clarify what is going on.
The real numbers
![]() under addition is a locally compact
topological group. Normalized Haar measure
under addition is a locally compact
topological group. Normalized Haar measure ![]() has the property
that
has the property
that
![]() , where
, where ![]() are real numbers and
are real numbers and
![]() is the closed interval from
is the closed interval from ![]() to
to ![]() . The subset
. The subset
![]() of
of
![]() is discrete, and the quotient
is discrete, and the quotient
![]() is a compact topological group, which thus
has a Haar measure. Let
is a compact topological group, which thus
has a Haar measure. Let
![]() be the Haar measure
on
be the Haar measure
on ![]() normalized so that the natural quotient
normalized so that the natural quotient
![]() preserves the measure, in the sense that if
preserves the measure, in the sense that if
![]() is a measurable set that maps injectively into
is a measurable set that maps injectively into ![]() , then
, then
![]() . This determine
. This determine
![]() and we have
and we have
![]() since
since
![]() is a measurable set that maps bijectively onto
is a measurable set that maps bijectively onto
![]() and has measure
and has measure ![]() . The situation for the map
. The situation for the map
![]() is pretty much the same.
is pretty much the same.
Whenever
![]() is such that
is such that
First we show that (20.4.1) implies that
![]() for almost all
for almost all ![]() . Because
. Because
![]() is an adele, we have
is an adele, we have
![]() for almost all
for almost all ![]() . If
. If
![]() for
infinitely many
for
infinitely many ![]() , then the product in (20.4.1) would
have to be 0. (We prove this only when
, then the product in (20.4.1) would
have to be 0. (We prove this only when ![]() is a finite extension of
is a finite extension of
![]() .) Excluding archimedean valuations, this is because the
normalized valuation
.) Excluding archimedean valuations, this is because the
normalized valuation
![]() , which if less
than
, which if less
than ![]() is necessarily
is necessarily ![]() . Any infinite product of numbers
. Any infinite product of numbers
![]() must be 0, whenever
must be 0, whenever ![]() is a sequence of primes.
is a sequence of primes.
Let ![]() be the Haar measure of
be the Haar measure of
![]() induced from normalized
Haar measure on
induced from normalized
Haar measure on ![]() , and let
, and let ![]() be the Haar measure of the set
of
be the Haar measure of the set
of
![]() that satisfy
that satisfy
Then
![]() since
since
![]() is compact, and
is compact, and
![]() because the number of archimedean valuations
because the number of archimedean valuations ![]() is finite. We show
that
is finite. We show
that
The set ![]() of
of
![]() such that
such that
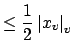 if if |
||
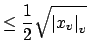 if if |
||
Because of (20.4.2), in
the quotient map
![]() there
must be a pair of distinct points of
there
must be a pair of distinct points of ![]() that have
the same image in
that have
the same image in
![]() , say
, say
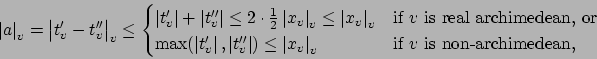
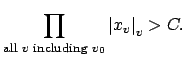
We proved before that ![]() is discrete in
is discrete in ![]() . If one valuation is
removed, the situation is much different.
. If one valuation is
removed, the situation is much different.
Recall that if
![]() then a basis of open
sets about
then a basis of open
sets about
![]() is the collection of products
is the collection of products
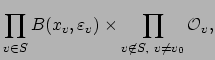
By the corollary to our proof that
![]() is compact
(Corollary 20.3.6), there is a
is compact
(Corollary 20.3.6), there is a
![]() that is
defined by inequalities of the form
that is
defined by inequalities of the form
![]() (where
(where
![]() for almost all
for almost all ![]() ) such that ever
) such that ever
![]() is of the form
is of the form
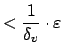 for for |
||
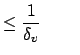 for for |
In the next chapter we'll introduce the ideles ![]() . Finally,
we'll relate ideles to ideals, and use everything so far to give a new
interpretation of class groups and their finiteness.
. Finally,
we'll relate ideles to ideals, and use everything so far to give a new
interpretation of class groups and their finiteness.
William Stein 2004-05-06