Next: Tensor Products Up: Normed Spaces and Tensor Previous: Normed Spaces and Tensor Contents Index
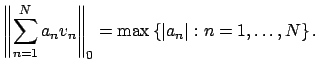
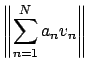 |
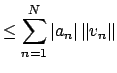 |
|
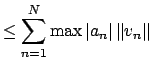 |
||
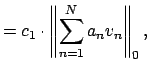 |
To finish the proof, we show that there is a
![]() such that for all
such that for all ![]() ,
,
By what we have already shown, the function
![]() is continuous
in the
is continuous
in the
![]() -topology, so by local compactness it attains its
lower bound
-topology, so by local compactness it attains its
lower bound ![]() on the unit circle
on the unit circle
![]() . (Why is the unit circle compact? With
respect to
. (Why is the unit circle compact? With
respect to
![]() , the topology on
, the topology on ![]() is the same as that of a
product of copies of
is the same as that of a
product of copies of ![]() . If the valuation is archimedean then
. If the valuation is archimedean then
![]() or
or
![]() with the standard topology and the unit circle is
compact. If the valuation is non-archimedean, then we saw (see
Remark 17.1.7) that if
with the standard topology and the unit circle is
compact. If the valuation is non-archimedean, then we saw (see
Remark 17.1.7) that if ![]() is locally compact, then
the valuation is discrete, in which case we showed that the unit disc
is compact, hence the unit circle is also compact since it is closed.)
Note that
is locally compact, then
the valuation is discrete, in which case we showed that the unit disc
is compact, hence the unit circle is also compact since it is closed.)
Note that ![]() by part 1 of Definition 18.1.1. Also,
by definition of
by part 1 of Definition 18.1.1. Also,
by definition of
![]() , for any
, for any ![]() there exists
there exists ![]() such that
such that
![]() (just take the max coefficient in our
basis). Thus we can write any
(just take the max coefficient in our
basis). Thus we can write any ![]() as
as ![]() where
where ![]() and
and ![]() with
with
![]() . We then have
. We then have
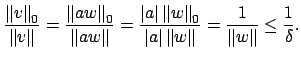
William Stein 2004-05-06