Next: Discriminants Up: Discrimannts, Norms, and Finiteness Previous: Discrimannts, Norms, and Finiteness Contents Index
The fact that
![]() is discrete in
is discrete in
![]() implies that
implies that
![]() has dimension equal to the rank
has dimension equal to the rank ![]() of
of
![]() , as claimed. This last assertion is not obvious, and
requires observing that if
, as claimed. This last assertion is not obvious, and
requires observing that if ![]() if a free abelian group that is
discrete in a real vector space
if a free abelian group that is
discrete in a real vector space ![]() and
and
![]() , then the rank of
, then the rank of
![]() equals the dimension of
equals the dimension of ![]() . Here's why this is true. If
. Here's why this is true. If
![]() are a basis for
are a basis for
![]() , then
, then
![]() has finite index in
has finite index in ![]() , since otherwise there would be
infinitely many elements of
, since otherwise there would be
infinitely many elements of ![]() in a fundamental domain for
in a fundamental domain for
![]() , which would contradict discreteness of
, which would contradict discreteness of ![]() . Thus
the rank of
. Thus
the rank of ![]() is
is
![]() , as claimed.
, as claimed.
![]()
Since
![]() is a lattice in
is a lattice in ![]() , the volume of
, the volume of
![]() is finite. Suppose
is finite. Suppose
![]() is a basis for
is a basis for
![]() . Then if
. Then if ![]() is the matrix whose
is the matrix whose ![]() th row is
th row is
![]() ,
then
,
then
![]() is the volume of
is the volume of
![]() . (Take this
determinant as the definition of the volume--we won't be using
``volume'' here except in a formal motivating way.)
. (Take this
determinant as the definition of the volume--we won't be using
``volume'' here except in a formal motivating way.)
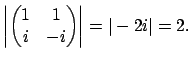
Let
![]() be the ring of integers of
be the ring of integers of
![]() .
The map
.
The map ![]() is
is
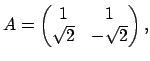
William Stein 2004-05-06