Next: is Noetherian Up: Commutative Algebra Previous: Commutative Algebra Contents Index
A of ![]() -modules
-modules
![]() is a abelian group
homomorphism such that for any
is a abelian group
homomorphism such that for any ![]() and
and ![]() we have
we have
![]() . A of
. A of ![]() -modules
-modules
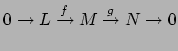
Notice that any submodule ![]() of
of ![]() is Noetherian, because if every submodule of
is Noetherian, because if every submodule of ![]() is finitely generated then so is every submodule of
is finitely generated then so is every submodule of ![]() , since submodules of
, since submodules of ![]() are also submodules of
are also submodules of ![]() .
.
![]() : Suppose 3 were false, so there exists
a nonempty set
: Suppose 3 were false, so there exists
a nonempty set ![]() of submodules of
of submodules of ![]() that does not contain a
maximal element. We will use
that does not contain a
maximal element. We will use ![]() to construct an infinite ascending
chain of submodules of
to construct an infinite ascending
chain of submodules of ![]() that does not stabilize. Note that
that does not stabilize. Note that ![]() is
infinite, otherwise it would contain a maximal element. Let
is
infinite, otherwise it would contain a maximal element. Let ![]() be
any element of
be
any element of ![]() . Then there is an
. Then there is an ![]() in
in ![]() that contains
that contains
![]() , otherwise
, otherwise ![]() would contain the maximal element
would contain the maximal element ![]() .
Continuing inductively in this way we find an
.
Continuing inductively in this way we find an ![]() in
in ![]() that
properly contains
that
properly contains ![]() , etc., and we produce an infinite ascending
chain of submodules of
, etc., and we produce an infinite ascending
chain of submodules of ![]() , which contradicts the ascending chain
condition.
, which contradicts the ascending chain
condition.
![]() : Suppose 1 is false, so there is a
submodule
: Suppose 1 is false, so there is a
submodule ![]() of
of ![]() that is not finitely generated. We will show
that the set
that is not finitely generated. We will show
that the set ![]() of all finitely generated submodules of
of all finitely generated submodules of ![]() does not
have a maximal element, which will be a contradiction. Suppose
does not
have a maximal element, which will be a contradiction. Suppose ![]() does have a maximal element
does have a maximal element ![]() . Since
. Since ![]() is finitely generated and
is finitely generated and
![]() , and
, and ![]() is not finitely generated, there is an
is not finitely generated, there is an ![]() such that
such that
![]() . Then
. Then ![]() is an element of
is an element of ![]() that
strictly contains the presumed maximal element
that
strictly contains the presumed maximal element ![]() , a contradiction.
, a contradiction.
![]()
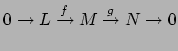
Next assume nothing about ![]() , but suppose that both
, but suppose that both ![]() and
and ![]() are
Noetherian. If
are
Noetherian. If ![]() is a submodule of
is a submodule of ![]() , then
, then
![]() is isomorphic to a submodule of the Noetherian module
is isomorphic to a submodule of the Noetherian module ![]() , so
, so ![]() is
generated by finitely many elements
is
generated by finitely many elements
![]() . The quotient
. The quotient
![]() is isomorphic (via
is isomorphic (via ![]() ) to a submodule of the Noetherian
module
) to a submodule of the Noetherian
module ![]() , so
, so ![]() is generated by finitely many elements
is generated by finitely many elements
![]() . For each
. For each ![]() , let
, let ![]() be a lift of
be a lift of ![]() to
to
![]() , modulo
, modulo ![]() . Then the elements
. Then the elements
![]() generate
generate ![]() , for if
, for if ![]() , then there is some element
, then there is some element ![]() such that
such that ![]() is an
is an ![]() -linear combination of the
-linear combination of the ![]() ,
and
,
and ![]() is an
is an ![]() -linear combination of the
-linear combination of the ![]() .
.
![]()
The rings
![]() and
and
![]() are
isomorphic, so it suffices to prove that if
are
isomorphic, so it suffices to prove that if ![]() is Noetherian then
is Noetherian then
![]() is also Noetherian. (Our proof follows
[Art91, §12.5].)
Thus suppose
is also Noetherian. (Our proof follows
[Art91, §12.5].)
Thus suppose ![]() is an ideal of
is an ideal of ![]() and that
and that ![]() is
Noetherian. We will show that
is
Noetherian. We will show that ![]() is finitely generated.
is finitely generated.
Let ![]() be the set of leading coefficients of polynomials in
be the set of leading coefficients of polynomials in ![]() along
with 0. If
along
with 0. If ![]() are nonzero with
are nonzero with ![]() , then there are
polynomials
, then there are
polynomials ![]() and
and ![]() in
in ![]() with leading coefficients
with leading coefficients ![]() and
and ![]() .
If
.
If
![]() , then
, then ![]() is the leading coefficient of
is the leading coefficient of
![]() , so
, so ![]() . If
. If ![]() and
and ![]() with
with ![]() , then
, then ![]() is the leading coefficient of
is the leading coefficient of ![]() , so
, so
![]() . Thus
. Thus ![]() is an ideal in
is an ideal in ![]() , so since
, so since ![]() is Noetherian
there exists
is Noetherian
there exists
![]() that generate
that generate ![]() as an ideal. Since
as an ideal. Since
![]() is the set of leading coefficients of elements of
is the set of leading coefficients of elements of ![]() , and the
, and the
![]() are in
are in ![]() , we can choose for each
, we can choose for each ![]() an element
an element ![]() with leading coefficient
with leading coefficient ![]() . By multipying the
. By multipying the ![]() by some power
of
by some power
of ![]() , we may assume that the
, we may assume that the ![]() all have the same degree
all have the same degree ![]() .
.
Let ![]() be the set of elements of
be the set of elements of ![]() that have degree strictly less
than
that have degree strictly less
than ![]() . This set is closed under addition and under multiplication by
elements of
. This set is closed under addition and under multiplication by
elements of ![]() , so
, so ![]() is a module over
is a module over ![]() . The module
. The module ![]() is submodule of
the
is submodule of
the ![]() -module of polynomials of degree less than
-module of polynomials of degree less than ![]() , which is
Noetherian because it is generated by
, which is
Noetherian because it is generated by
![]() . Thus
. Thus
![]() is finitely generated, and we may choose generators
is finitely generated, and we may choose generators
![]() for
for ![]() .
.
Suppose ![]() is an arbitrary element. We will show by induction
on the degree of
is an arbitrary element. We will show by induction
on the degree of ![]() that
that ![]() is an
is an ![]() -linear combination of
-linear combination of
![]() . Thus suppose this statement is
true for all elements of
. Thus suppose this statement is
true for all elements of ![]() of degree less than the degree of
of degree less than the degree of ![]() .
If the degree of
.
If the degree of ![]() is less than
is less than ![]() , then
, then
![]() , so
, so ![]() is
in the
is
in the ![]() -ideal generated by
-ideal generated by
![]() . Next suppose
that
. Next suppose
that ![]() has degree
has degree ![]() . Then the leading coefficient
. Then the leading coefficient ![]() of
of ![]() lies in the ideal
lies in the ideal ![]() of leading coefficients of
of leading coefficients of ![]() , so there
exist
, so there
exist ![]() such that
such that
![]() . Since
. Since
![]() has leading coefficient
has leading coefficient ![]() , the difference
, the difference
![]() has degree less than the degree
has degree less than the degree ![]() of
of ![]() . By induction
. By induction
![]() is an
is an ![]() linear combination of
linear combination of
![]() , so
, so ![]() is also an
is also an ![]() linear combination of
linear combination of
![]() . Since each
. Since each ![]() and
and ![]() lies in
lies in
![]() , it follows that
, it follows that ![]() is generated by
is generated by
![]() , so
, so ![]() is finitely generated, as required.
is finitely generated, as required.
![]()
Properties of Noetherian rings and modules will be crucial in the rest of this course. We have proved above that Noetherian rings have many desirable properties.