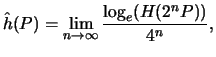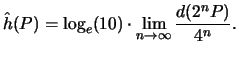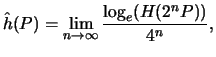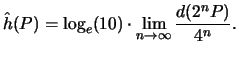Next: About this document ...
Up: Freshman Seminar 21n: Elliptic
Previous: Reading Assignment
- (Jenna)
Prove that the set of rational numbers
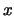 with height
with height 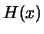 less than
less than 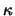 contains at most
contains at most
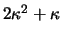 elements.
elements.
- (Jeff)
Let
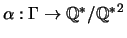 be the map defined
in Section 5 of Chapter III of [Silverman-Tate] by the rule
be the map defined
in Section 5 of Chapter III of [Silverman-Tate] by the rule
Prove that if
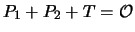 , then
, then
- (Jeff/Mauro)
Let
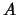 and
and 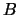 be abelian groups and let
be abelian groups and let
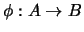 and
and
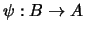 be homomorphisms. Suppose there is an integer
be homomorphisms. Suppose there is an integer
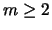 such that
such that
Suppose further that 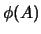 has finite index in
has finite index in 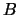 ,
and
,
and 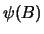 has finite index in
has finite index in 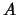 .
.
- (Jeff) Prove that
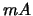 has finite index in
has finite index in 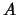 , and that
the index satisfies the inequality
, and that
the index satisfies the inequality
- (Mauro) Give an example to show that it is possible for
the inequality in (a) to be a strict inequality.
- (Jennifer)
Let
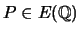 be a point on an elliptic curve.
The canonical height of
be a point on an elliptic curve.
The canonical height of 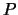 is
where
is
where 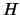 is as in Chapter III of [Silverman-Tate].
Define a function
is as in Chapter III of [Silverman-Tate].
Define a function
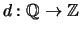 by letting
by letting 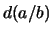 be the maximum of the number of digits of
be the maximum of the number of digits of 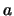 and
and 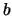 (where
we assume
(where
we assume
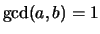 ), and extend
), and extend 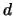 to points
to points 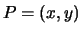 by letting
by letting
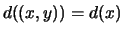 . Prove that
. Prove that



Next: About this document ...
Up: Freshman Seminar 21n: Elliptic
Previous: Reading Assignment
William A Stein
2003-03-04
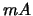 has finite index in
has finite index in 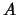 , and that
the index satisfies the inequality
, and that
the index satisfies the inequality
![$\displaystyle [A:mA] \leq [A:\psi(B)]\cdot [B:\phi(A)].
$](img35.png)