


Next: Reading Assignment
Up: Freshman Seminar 21n: Elliptic
Previous: Freshman Seminar 21n: Elliptic
Your reading this week and next is about Mordell's theorem, which
is the assertion that the Mordell-Weil group
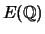 of an elliptic
curve is finitely generated. In simpler terms, given any elliptic curve
of an elliptic
curve is finitely generated. In simpler terms, given any elliptic curve  over
over
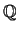 there are points
there are points
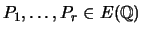 such that
Though it is an open problem to give a provably correct algorithm to
compute a finite generating set
such that
Though it is an open problem to give a provably correct algorithm to
compute a finite generating set
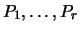 , in practice we can
usually do this, and we'll learn a little about how in the next two
weeks.
, in practice we can
usually do this, and we'll learn a little about how in the next two
weeks.
This week's reading and problems are very theoretical; next
week's reading is example oriented and more computational.
Where are we going? After finishing chapter III, we'll study chapter IV
about elliptic curves over finite fields and the elliptic curve
factorization method. After Spring Break, we'll use the foundations
we've developed, guided by your interests, to investigate some of the
following topics: modularity of elliptic curves; connection between
elliptic curves and Fermat's Last theorem; the Birch and
Swinnerton-Dyer conjecture; cryptographic applications of elliptic
curves; historical emergence of elliptic curves.



Next: Reading Assignment
Up: Freshman Seminar 21n: Elliptic
Previous: Freshman Seminar 21n: Elliptic
William A Stein
2003-03-04