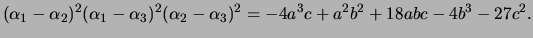Next: About this document ...
Up: New reading and problems
Previous: New reading and problems
- (Jenna)
Let
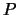 ,
, 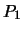 ,
, 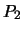 ,
, 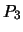 be points in
be points in 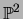 and let
and let 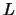 be a line in
be a line in 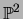 .
.
- If
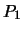 ,
, 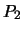 , and
, and 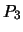 do not lie on a line, prove
that there is a projective transformation of
do not lie on a line, prove
that there is a projective transformation of 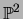 so that
so that
- If no three of
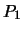 ,
, 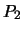 ,
, 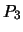 and
and 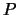 lie on a line,
prove that there is a unique projective transformation as in
(a) which also sends
lie on a line,
prove that there is a unique projective transformation as in
(a) which also sends 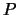 to
to 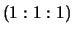 .
.
- Prove that if
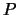 does not lie on
does not lie on 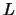 , then there is a projective
transformation of
, then there is a projective
transformation of 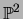 so that
so that 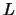 is sent to the line
is sent to the line 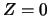 and
and 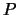 is sent to the point
is sent to the point 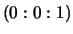 .
.
- (Jennifer)
Let
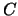 be the cubic curve
be the cubic curve 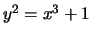 .
.
- For each prime
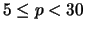 , describe the group
, describe the group
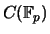 of points on this curve having coordinates in the finite field of order
of points on this curve having coordinates in the finite field of order 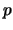 .
(Use a computer.)
.
(Use a computer.)
- For each prime in (a), let
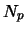 be the number of points in
be the number of points in
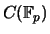 . (Don't forget the point at infinity.) For the set of
primes satisfying
. (Don't forget the point at infinity.) For the set of
primes satisfying
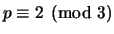 , can you see a pattern for the
values of
, can you see a pattern for the
values of 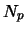 ? Make a general conjecture about the value of
? Make a general conjecture about the value of 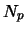 when
when
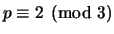 and prove that your conjecture is correct.
and prove that your conjecture is correct.
- Find a conjectural pattern for the values of
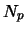 for the set
of primes
for the set
of primes
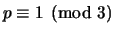 , and give evidence for your conjecture.
Feel free to try to find the answer to this question by looking in
other books or asking around the department, since this problem is
double starred in Silverman-Tate.
, and give evidence for your conjecture.
Feel free to try to find the answer to this question by looking in
other books or asking around the department, since this problem is
double starred in Silverman-Tate.
- (Mauro)
Let
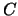 be a nonsingular cubic curve given by a Weierstrass equation
be a nonsingular cubic curve given by a Weierstrass equation
- Prove that
Deduce that a point
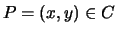 is a point
of order three if and only if
is a point
of order three if and only if 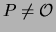 and
and 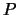 is a point
of inflection on the curve
is a point
of inflection on the curve 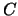 .
.
- Suppose that
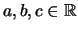 . Prove that
. Prove that 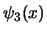 has exactly two real roots, say
has exactly two real roots, say
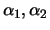 with
with
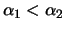 . Prove that
. Prove that
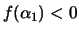 and
and
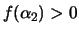 . Deduce that the points
in
. Deduce that the points
in
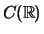 of order dividing
of order dividing 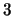 form a cyclic group of
order
form a cyclic group of
order 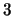 .
.
- (Alex)
Let
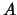 be an abelian group, and for every integer
be an abelian group, and for every integer 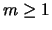 ,
let
,
let ![$ A[m]$](img39.png) be the set of elements
be the set of elements 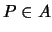 satisfying
satisfying 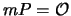 .
(Note that
.
(Note that ![$ A[m]$](img39.png) is denoted
is denoted 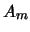 in [Silverman-Tate].)
in [Silverman-Tate].)
- Prove that
![$ A[m]$](img39.png) is a subgroup of
is a subgroup of 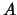 .
.
- Suppose that
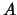 has order
has order 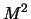 and that for every integer
and that for every integer 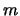 dividing
dividing 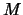 , the subgroup
, the subgroup ![$ A[m]$](img39.png) has order
has order 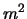 . Prove that
. Prove that 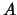 is the direct product of two cyclic groups of order
is the direct product of two cyclic groups of order 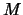 .
.
- Find an example of a non-abelian group
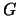 and an integer
and an integer 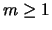 so that the set
so that the set
![$ G[m] = \{g \in G : g^m = 1\}$](img47.png) is not
a subgroup of
is not
a subgroup of 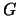 .
.
- (Jeff)
- Let
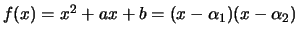 be a quadratic
polynomial with the indicated factorization. Prove that
be a quadratic
polynomial with the indicated factorization. Prove that
- Let
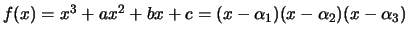 be a cubic polynomial with the
indicated factorization. Prove that
be a cubic polynomial with the
indicated factorization. Prove that



Next: About this document ...
Up: New reading and problems
Previous: New reading and problems
William A Stein
2003-02-18
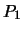 ,
, 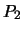 , and
, and 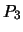 do not lie on a line, prove
that there is a projective transformation of
do not lie on a line, prove
that there is a projective transformation of 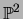 so that
so that
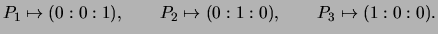
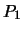 ,
, 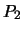 ,
, 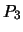 and
and 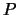 lie on a line,
prove that there is a unique projective transformation as in
(a) which also sends
lie on a line,
prove that there is a unique projective transformation as in
(a) which also sends 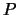 to
to 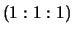 .
.
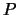 does not lie on
does not lie on 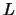 , then there is a projective
transformation of
, then there is a projective
transformation of 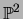 so that
so that 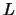 is sent to the line
is sent to the line 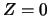 and
and 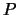 is sent to the point
is sent to the point 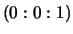 .
.
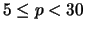 , describe the group
, describe the group
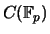 of points on this curve having coordinates in the finite field of order
of points on this curve having coordinates in the finite field of order 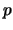 .
(Use a computer.)
.
(Use a computer.)
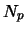 be the number of points in
be the number of points in
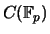 . (Don't forget the point at infinity.) For the set of
primes satisfying
. (Don't forget the point at infinity.) For the set of
primes satisfying
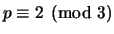 , can you see a pattern for the
values of
, can you see a pattern for the
values of 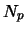 ? Make a general conjecture about the value of
? Make a general conjecture about the value of 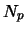 when
when
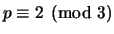 and prove that your conjecture is correct.
and prove that your conjecture is correct.
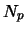 for the set
of primes
for the set
of primes
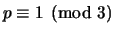 , and give evidence for your conjecture.
Feel free to try to find the answer to this question by looking in
other books or asking around the department, since this problem is
double starred in Silverman-Tate.
, and give evidence for your conjecture.
Feel free to try to find the answer to this question by looking in
other books or asking around the department, since this problem is
double starred in Silverman-Tate.
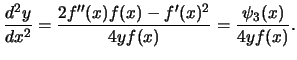
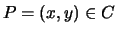 is a point
of order three if and only if
is a point
of order three if and only if 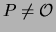 and
and 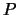 is a point
of inflection on the curve
is a point
of inflection on the curve 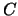 .
.
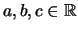 . Prove that
. Prove that 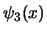 has exactly two real roots, say
has exactly two real roots, say
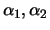 with
with
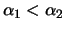 . Prove that
. Prove that
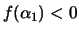 and
and
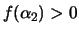 . Deduce that the points
in
. Deduce that the points
in
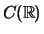 of order dividing
of order dividing 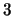 form a cyclic group of
order
form a cyclic group of
order 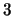 .
.
![$ A[m]$](img39.png) is a subgroup of
is a subgroup of 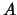 .
.
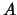 has order
has order 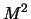 and that for every integer
and that for every integer 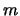 dividing
dividing 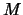 , the subgroup
, the subgroup ![$ A[m]$](img39.png) has order
has order 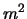 . Prove that
. Prove that 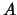 is the direct product of two cyclic groups of order
is the direct product of two cyclic groups of order 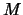 .
.
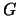 and an integer
and an integer 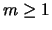 so that the set
so that the set
![$ G[m] = \{g \in G : g^m = 1\}$](img47.png) is not
a subgroup of
is not
a subgroup of 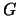 .
.
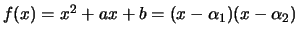 be a quadratic
polynomial with the indicated factorization. Prove that
be a quadratic
polynomial with the indicated factorization. Prove that
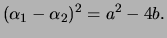
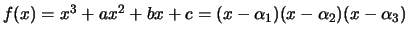 be a cubic polynomial with the
indicated factorization. Prove that
be a cubic polynomial with the
indicated factorization. Prove that