
Math 252: Modular Abelian Varieties
Let D be the fundamental domain for G=PSL2(Z) that I described in the last lecture, which is illustrated below:

Last time we proved that if z is any point in the upper half plane, then there is an element g in G such that g(z) is in D. The proof was nonconstructive. Here is an algorithm to find such a g in practice.
Do the following until z is in D: |
This process must terminate, because in step 2 the imaginary part of -1/z is bigger than the imaginary part of z, and the proof from last time showed that the imaginary parts of the conjugates of z are bounded above.
Remarks.
Note that this algorithm also gives an algorithm to write an arbitrary element of G in terms of
![]() and
and ![]() .
.
For example, suppose ![]() .
Hit 2i by g, then find a combination of S and T that conjugates g back into
D. We get
.
Hit 2i by g, then find a combination of S and T that conjugates g back into
D. We get
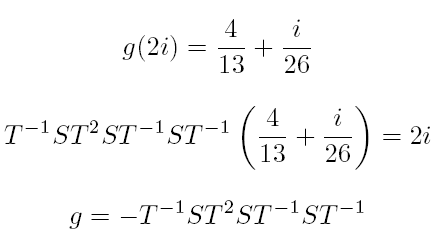
Remark. If you wanted to do computations like this efficiently, you would obtain the representation of g from the partial convergents of the continued fraction of a/b, where a and b are the entries in the first column of g. See the end of Section 2.1 of Cremona's book for enough of a hint as to what to do.
As you will show in your homework reduction modulo N is surjective, so we have an exact sequence
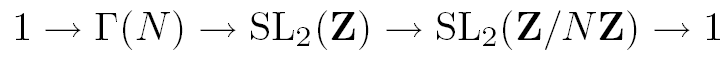
DEFINITION: The group ![]() is by definition the kernel of the reduction map. It is called the principal
congruence subgroup of level N. A congruence subgroup
is any subgroup of SL2(Z) that contains
is by definition the kernel of the reduction map. It is called the principal
congruence subgroup of level N. A congruence subgroup
is any subgroup of SL2(Z) that contains ![]() for some N.
for some N.
It is clear that any congruence subgroup has finite index, since
![]() does. What about
the converse? This is the so-called "congruence subgroup problem."
According to this MathSciNet review, if p
is a prime, then every finite index subgroup of SL2(Z[1/p])
is a congruence subgroup, and for any n>2, all finite index subgroups
of SL2(Z) are congruence subgroups. However, there
are plenty of finite index subgroups of SL2(Z) that
are not congruence subgroups. This
paper by Hsu contains an algorithm to decide if a finite index subgroup
is a congruence subgroup, and gives an example of a subgroup of index 12 that
it is not a congruence subgroup. Also this MathSciNet
review of a paper by Thompson is about his proof of a surprising conjecture
of Atkin about modular forms for noncongruence subgroups.
does. What about
the converse? This is the so-called "congruence subgroup problem."
According to this MathSciNet review, if p
is a prime, then every finite index subgroup of SL2(Z[1/p])
is a congruence subgroup, and for any n>2, all finite index subgroups
of SL2(Z) are congruence subgroups. However, there
are plenty of finite index subgroups of SL2(Z) that
are not congruence subgroups. This
paper by Hsu contains an algorithm to decide if a finite index subgroup
is a congruence subgroup, and gives an example of a subgroup of index 12 that
it is not a congruence subgroup. Also this MathSciNet
review of a paper by Thompson is about his proof of a surprising conjecture
of Atkin about modular forms for noncongruence subgroups.
Since ![]() is a kernel, it is a normal subgroup. There are two other extremely popular
families of congruence subgroups, neither of which are normal:
is a kernel, it is a normal subgroup. There are two other extremely popular
families of congruence subgroups, neither of which are normal:
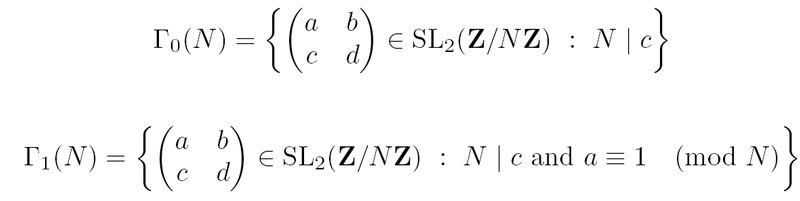
Helena Verrill's fundamental domains program draws fundamental domains. You should probably look through her description of the interesting mathematical algorithms used in the program. Here are three screen shots, which illustrates some fundamental domains.
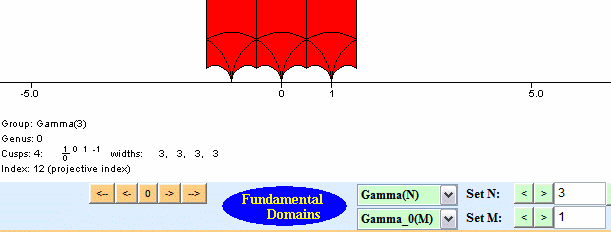
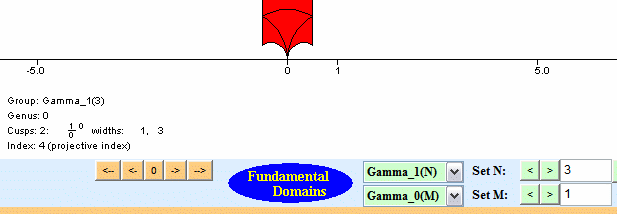
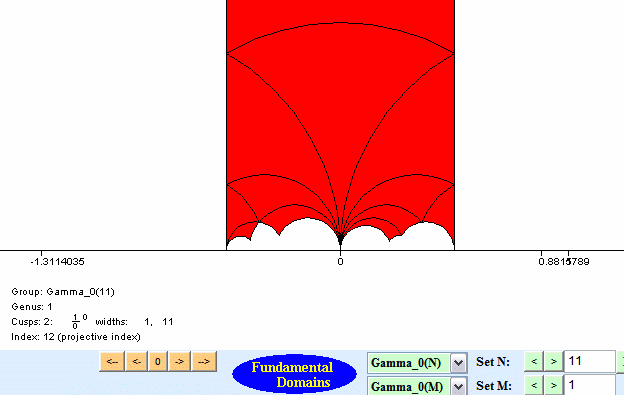
The program works by finding right coset representatives for the congruence subgroup in SL2(Z), and translating around a fundamental domain for SL2(Z). The coset representatives are chosen, as described in Verrrill's paper, so that the domain is connected and not tiny -- it wouldn't be interesting to draw a fundamental that consists of a few dots on the screen, even though it might be accurate!
Finding coset representatives for any of the three families of congruence subgroups
mentioned above is relatively straightforward. To make the problem easy to think
about, note that you can quotient out by ![]() first. Then the question amounts to finding coset representatives for a subgroup
of SL2(Z), which is reasonably straightforward.
For example:
first. Then the question amounts to finding coset representatives for a subgroup
of SL2(Z), which is reasonably straightforward.
For example:
Proposition. The coset representatives for Gamma_0(N) are in natural bijection with the elements of P1(Z/NZ).
Let G be a finite index subgroup of SL2(Z). Let R be a set of coset representatives for G. Define maps s and t from R to G as follows. If r in R then there exists a unique r' in R such that GrS = Gr'. Let s(r) = rS(r')^(-1). Likewise, there is a unique r' such that GrT = Gr' and we let t(r) = rT(r')^(-1). Note that s(r) and t(r) are in G for all r.
Proposition. G is generated by the union of s(R) and t(R).
Proof. Omited.
There are much more sophisticated algorithms that use group actions on trees. Verrill implemented much of this in MAGMA, but unfortunately I don't have time to talk about it today.
Next week we will consider the quotient of the upper half plane by the action of a congruence subgroup. This quotient space is a noncompact Riemann surface. The missing cusps are in bijection with the orbits of the action of the congruence subgroup on P1(Q). Adding them in we obtain a compact Riemann surface. On Monday we'll construct this Riemann surface, and discuss some of its properties. On Wednesday, we'll talk about how to represent its homology using modular symbols. On Friday, we'll describe a finite presentation for homology that is due to Yuri Manin, and sketch his proof that the presentation is correct.