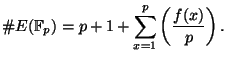Next: About this document ...
Math 124 Final Examination
Due Sunday 12 January 2003 by 5pm
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2002
Fall 2002
This is the Fall 2002 Math 124 take-home final
examination. You may not discuss the problems with anyone. You
are allowed to look at books, course notes, web pages, and use a
computer (MAGMA, Maple, etc.), but you must acknowledge any sources that you
use. If you find the complete solution to one of these problems in a
book, then good job--you are allowed to copy it.
For your convenience, the complete course notes are available as
a single file at
http://modular.fas.harvard.edu/edu/Fall2002/124/stein/.
All problems are worth the same number of points (e.g., problems 2 and
3 are worth the same number of points). Choose and do EXACTLY 8 of the following  problems (e.g., all parts of
problems 1, 2, 3, 5, 6, 10, 11, 12 ). Choose wisely; some
problems might be easy, others difficult open problems, and
some might ask you to prove something that is false (say what is wrong
with the problem for full credit). At least eight are not open
problems! Clearly indicate which problem you are attempting and which
you are omiting.
problems (e.g., all parts of
problems 1, 2, 3, 5, 6, 10, 11, 12 ). Choose wisely; some
problems might be easy, others difficult open problems, and
some might ask you to prove something that is false (say what is wrong
with the problem for full credit). At least eight are not open
problems! Clearly indicate which problem you are attempting and which
you are omiting.
If you have trouble getting into the math department to hand in your
exam, call my office phone (617-495-1790)
or my mobile phone (617-308-0144) so I can open the door.
- The usual Euler
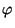 function is a map
function is a map
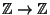 . Fix a prime number
. Fix a prime number 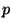 , and define
a polynomial analogue of Euler's function
by
, and define
a polynomial analogue of Euler's function
by
(let 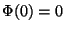 ).
Thus, e.g., if
).
Thus, e.g., if 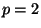 then
then
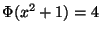 .
Say that polynomials
.
Say that polynomials
![$ f(x), g(x)\in \mathbb{F}_p[x]$](img10.png) are coprime if
that is,
are coprime if
that is, 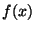 and
and 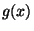 have
no common roots in
have
no common roots in
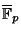 .
.
- Prove that
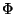 is multiplicative, in the sense that
if
is multiplicative, in the sense that
if 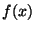 and
and 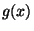 are coprime, then
are coprime, then
- The Euler
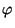 function does not satisfy
function does not satisfy
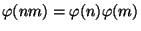 for all integers
for all integers 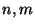 ; for example,
; for example,
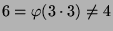 .
Does
.
Does 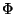 satisfy
satisfy
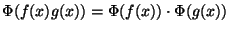 for all polynomials
for all polynomials 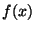 and
and 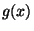 ? Give a proof or
counterexample.
? Give a proof or
counterexample.
Write an insightful review of the book Uncle Petros and
Goldbach's Conjecture. (Your intended audience is a ``typical
Harvard undergraduate with greater than usual interest in
mathematics'', and your review should be at least one page
long.)
- Characterize the positive integers
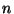 such that
such that
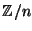 is a field.
is a field.
- Characterize the positive integers
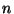 such that
such that
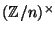 is cyclic.
is cyclic.
- Characterize the positive integers
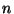 such that
such that 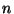 is a sum of two rational squares.
is a sum of two rational squares.
- Characterize the positive integers
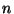 such that
such that 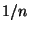 is a sum of two rational squares.
is a sum of two rational squares.
At a conference at the American Institute of Mathematics, Victor
Rotger from Barcelona asked me a question about primes. Call a prime
number 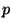 Victor if for every prime
Victor if for every prime
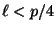 with
with
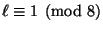 , we have
, we have
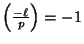 (that's the quadratic residue
symbol). Victor's Question: Are there infinitely many Victor primes?
Do numerical computations and formulate an intelligent response to
Victor's question. (You don't have to prove anything to get full
credit on this problem; just compute and give a reasonably intelligent
interpretation of what you find.)
(that's the quadratic residue
symbol). Victor's Question: Are there infinitely many Victor primes?
Do numerical computations and formulate an intelligent response to
Victor's question. (You don't have to prove anything to get full
credit on this problem; just compute and give a reasonably intelligent
interpretation of what you find.)
- Factor the integer
as a product
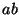 with
with 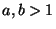 .
.
- Factor the integer
as a product
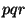 with
with 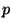 ,
, 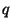 ,
, 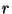 integers
integers 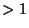 . You may use that
and
where
. You may use that
and
where 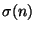 is the sum of the divisors of
is the sum of the divisors of 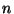 .
.
- Find a rational number
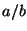 with
with
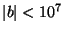 such that
such that
- Find three distinct solutions to
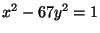 with
with 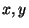 positive integers.
positive integers.
- Let
![$ f=ax^2+bxy+cy^2\in\mathbb{Z}[x,y]$](img44.png) be a quadratic form
whose discriminant
be a quadratic form
whose discriminant 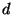 is a perfect square, possibly 0.
Show that
is a perfect square, possibly 0.
Show that 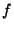 factors as
factors as
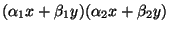 .
.
- Let
![$ f=ax^2+bxy+cy^2\in\mathbb{Z}[x,y]$](img44.png) be a quadratic form.
Show that there exists
be a quadratic form.
Show that there exists 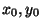 not both zero such that
not both zero such that
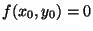 if and only if the discriminant of
if and only if the discriminant of 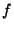 is
a perfect square.
is
a perfect square.
- Divide the following set of
binary quadratic forms up into equivalence classes
modulo the action of
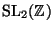 :
:
- Compute the discriminant of the ring of integers of
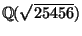 .
.
Consider a right triangle the lengths of whose sides are integers.
Prove that the area cannot be a perfect square.
Assume the truth of Fermat's last theorem. Deduce that
there is no right triangle with rational side lengths and area 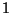 .
.
- Does
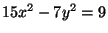 have a solution in the integers?
have a solution in the integers?
- Does
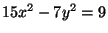 have a solution in the rational numbers?
have a solution in the rational numbers?
- Does
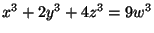 have any nontivial rational
solution?
have any nontivial rational
solution?
- Does
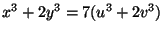 have any nontrivial rational
solutions?
have any nontrivial rational
solutions?
- Show that there are no positive integers
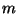 and
and 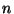 such
that
such
that 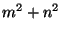 and
and 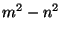 are both perfect squares.
are both perfect squares.
- Suppose
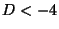 is a square-free integer, let
is a square-free integer, let
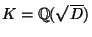 and let
and let 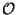 be the ring of integers in
be the ring of integers in 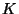 . Prove that the group
of units in
. Prove that the group
of units in 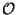 has order
has order 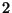 .
.
- For which squarefree integers
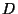 is the
prime
is the
prime 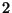 ramified in
ramified in
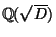 ?
(We say that
?
(We say that 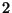 ramifies in
ramifies in
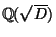 if
if
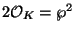 for
some prime
for
some prime 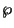 of
of 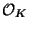 .)
.)
Some elliptic curve questions:
- Show that the number of pairs
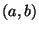 with
with
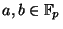 such that
such that
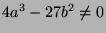 is exactly
is exactly 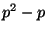 .
.
- Suppose
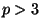 and
and
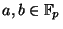 are such that
are such that
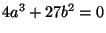 with
with
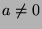 . Let
. Let 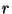 be the unique solution to
be the unique solution to 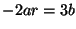 . Show
that
. Show
that 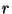 is a repeated root of the polynomial
is a repeated root of the polynomial 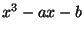 .
.
- Suppose that the polynomial
![$ f(x)=x^3+ax+b\in\mathbb{F}_p[x]$](img81.png) has no
repeated roots, and let
has no
repeated roots, and let 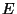 be the elliptic curve over
be the elliptic curve over
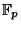 defined
by
defined
by 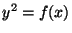 . Show that
. Show that



Next: About this document ...
William A Stein
2003-01-08
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2002
Fall 2002![]() problems (e.g., all parts of
problems 1, 2, 3, 5, 6, 10, 11, 12 ). Choose wisely; some
problems might be easy, others difficult open problems, and
some might ask you to prove something that is false (say what is wrong
with the problem for full credit). At least eight are not open
problems! Clearly indicate which problem you are attempting and which
you are omiting.
problems (e.g., all parts of
problems 1, 2, 3, 5, 6, 10, 11, 12 ). Choose wisely; some
problems might be easy, others difficult open problems, and
some might ask you to prove something that is false (say what is wrong
with the problem for full credit). At least eight are not open
problems! Clearly indicate which problem you are attempting and which
you are omiting.
![]() function is a map
function is a map
![]() . Fix a prime number
. Fix a prime number ![]() , and define
a polynomial analogue of Euler's function
by
, and define
a polynomial analogue of Euler's function
by
![]() Victor if for every prime
Victor if for every prime
![]() with
with
![]() , we have
, we have
![]() (that's the quadratic residue
symbol). Victor's Question: Are there infinitely many Victor primes?
Do numerical computations and formulate an intelligent response to
Victor's question. (You don't have to prove anything to get full
credit on this problem; just compute and give a reasonably intelligent
interpretation of what you find.)
(that's the quadratic residue
symbol). Victor's Question: Are there infinitely many Victor primes?
Do numerical computations and formulate an intelligent response to
Victor's question. (You don't have to prove anything to get full
credit on this problem; just compute and give a reasonably intelligent
interpretation of what you find.)
![]() .
.