



Next: About this document ...
Up: Lecture 9: The RSA
Previous: A Bigger Example in
Contents
Nikita's public key is 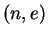 .
If we compute the factorization of
.
If we compute the factorization of 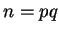 , then we can compute
, then we can compute
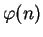 and hence deduce her secret decoder number
and hence deduce her secret decoder number 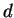 .
.
It is no easier to
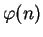 than to factor
than to factor 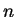 :
:
Suppose 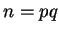 . Given
. Given
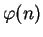 , it is very easy to
compute
, it is very easy to
compute 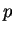 and
and 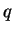 . We have
. We have
so we know 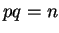 and
and
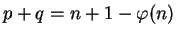 .
Thus we know the polynomial
whose roots are
.
Thus we know the polynomial
whose roots are 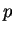 and
and 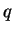 .
.
There is also a more complicated ``probabilistic algorithm'' to
find 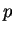 and
and 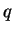 given the secret decoding number
given the secret decoding number 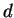 . I might
describe it in the next lecture.
. I might
describe it in the next lecture.
William A Stein
2001-10-01
![]() than to factor
than to factor ![]() :
:
![]() . Given
. Given
![]() , it is very easy to
compute
, it is very easy to
compute ![]() and
and ![]() . We have
. We have
![]() and
and ![]() given the secret decoding number
given the secret decoding number ![]() . I might
describe it in the next lecture.
. I might
describe it in the next lecture.