


Next: Multiplicative Functions
Up: Lecture 6: Congruences, Part
Previous: Wilson's Theorem
Sun Tsu Suan-Ching (4th century AD):
There are certain things whose number is unknown. Repeatedly divided
by 3, the remainder is 2; by 5 the remainder is 3; and by 7 the
remainder is 2. What will be the number?
In modern notation, Sun is asking us to solve the following system of
equations:
The Chinese Remainder Theorem asserts that a solution to Sun's
question exists, and the proof gives a method to find a solution.
Theorem 2.1 (The Chinese Remainder Theorem)
Let
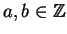
and
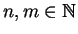
such that
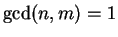
. Then there exists
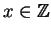
such that
Proof.
The equation
has a solution
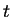
since
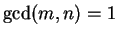
.
Set
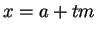
. We next verify that
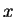
is a solution to the two equations.
Then
and

Now we can solve Sun's problem:
First, we use the theorem to find a solution to the pair
of equations
Set 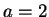 ,
, 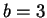 ,
, 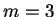 ,
, 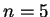 .
Step 1 is to find a solution to
.
Step 1 is to find a solution to
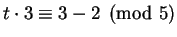 .
A solution is
.
A solution is 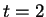 . Then
. Then
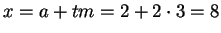 .
Since any
.
Since any 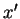 with
with
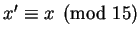 is also a solution to
those two equations, we can solve all three equations by
finding a solution to the pair of equations
is also a solution to
those two equations, we can solve all three equations by
finding a solution to the pair of equations
Again, we find a solution to
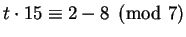 .
A solution is
.
A solution is 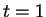 , so
Note that there are other solutions. Any
, so
Note that there are other solutions. Any
 is also a solution; e.g.,
is also a solution; e.g.,
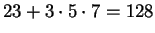 .
.
We can also solve Sun's problem in PARI:
? chinese(Mod(2,3),Mod(3,5))
%13 = Mod(8, 15)
? chinese(Mod(8,15),Mod(2,7))
%14 = Mod(23, 105)



Next: Multiplicative Functions
Up: Lecture 6: Congruences, Part
Previous: Wilson's Theorem
William A Stein
2001-09-23