


Next: What happened?
Up: Fermat's Little Theorem
Previous: Fermat's Little Theorem
The set of invertible elements of
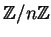 is a group
This group has order
is a group
This group has order
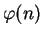 .
Theorem 4.3 asserts that the
order of an element of
.
Theorem 4.3 asserts that the
order of an element of
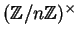 divides the order
divides the order
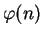 of
of
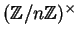 . This is a special case of the
more general theorem that if
. This is a special case of the
more general theorem that if 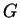 is a finite group and
is a finite group and 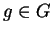 ,
then the order of
,
then the order of 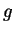 divide
divide 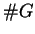 .
.
William A Stein
2001-09-20