Suppose ![]() with
with ![]() , say. Then
, say. Then
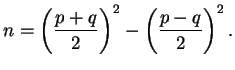
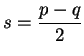
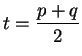
If ![]() , then
, then
![]() .
.
If ![]() , then
, then
![]() .
.
If ![]() , then
, then
![]() .
.
Thus ![]() . We find that
. We find that
![]() and
and
![]() .
.
tex2html_preform ? n=23360947609 %1 = 23360947609 ? sqrt(n) %2 = 152842.8853725288712694157797 ? x=%2 %3 = 152842.8853725288712694157797 ? floor(x+1) %4 = 152843 ? t=floor(x+1) %5 = 152843 ? t^2-n %6 = 35040 ? sqrt(t^2-n) %7 = 187.1897433087614445431082470 ? t++ %8 = 152844 ? sqrt(t^2-n) %9 = 583.7182539547654063924081356 ? t++ %10 = 152845 ? sqrt(t^2-n) %11 = 804.0000000000000000000000000 ? s=804 %12 = 804 ? p=t+s %13 = 153649 ? q=t-s %14 = 152041 ? p*q %15 = 23360947609 ? n %16 = 23360947609 ? factor(n) %17 = [152041 1] [153649 1]
Here is a bigger example in PARI:
? q=nextprime(random(10^50))
%20 = 78177096444230804504075122792410749354743712880803
? p=nextprime(q+1) \\ a nearby prime
%21 = 78177096444230804504075122792410749354743712880899
? n=p*q
%22 = 6111658408450564697085634201845976850509908580949986889525704...
...259650342157399279163289651693722481897
? t=floor(sqrt(n))+1
*** precision loss in truncation
? \p150 \\ set precision of floating-point computations.
realprecision = 154 significant digits (150 digits displayed)
? t=floor(sqrt(n))+1
%29 = 78177096444230804504075122792410749354743712880851
? sqrt(t^2-n)
%30 = 48.000000000000000000000000000000000000000000000000000000....
? s=48
%31 = 48
? t + s \\ p
%33 = 78177096444230804504075122792410749354743712880899
? t - s \\ q
%35 = 78177096444230804504075122792410749354743712880803