


Next: About this document ...
Homework 9: Elliptic Curves
DUE WEDNESDAY, NOVEMBER 28
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
There are 5 problems. Choose 4 of the 5 problems and
clearly indicate which ones you will be graded on (as usual,
your score will be a fraction between 0 and 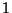 ).
As usual, you may use PARI for any of them, as long as
you explain what you are doing. Work in
groups.
).
As usual, you may use PARI for any of them, as long as
you explain what you are doing. Work in
groups.
- 1.
- (10 points) Let
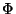 be the set of the
be the set of the 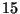 possible groups of
the form
possible groups of
the form
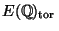 for
for 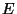 an elliptic curve over
an elliptic curve over
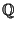 (see
Lecture 27). For each group
(see
Lecture 27). For each group 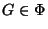 , if possible, find a finite
field
, if possible, find a finite
field
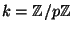 and an elliptic curve
and an elliptic curve 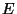 over
over 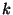 such that
such that
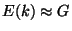 . (Hint: It is a fact that
. (Hint: It is a fact that
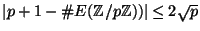 , so you only have to try
finitely many
, so you only have to try
finitely many 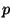 to show that a group
to show that a group 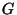 does not occur as the group
of points on an elliptic curve over a finite field.)
does not occur as the group
of points on an elliptic curve over a finite field.)
- 2.
- (6 points) Many number theorists, such as myself one week ago,
incorrectly think that Lutz-Nagell works well in practice.
Describe the steps you would
take if you were to use the Lutz-Nagell theorem
(Lecture 27) to compute the torsion subgroup of the elliptic
curve
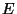 defined by the equation
then tell me why it would be very time consuming to actually
carry these steps out. Find the torsion subgroup of
defined by the equation
then tell me why it would be very time consuming to actually
carry these steps out. Find the torsion subgroup of 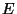 using the elltors command in PARI. Does elltors
use the Lutz-Nagell algorithm by default?
using the elltors command in PARI. Does elltors
use the Lutz-Nagell algorithm by default?
- 3.
- (6 points) Let
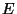 be the elliptic curve
defined by the equation
be the elliptic curve
defined by the equation
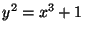 .
.
- (i)
- For each prime
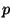 with
with
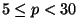 , describe the group
of points on this curve having coordinates in the finite field
, describe the group
of points on this curve having coordinates in the finite field
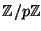 . (You can just give the order of each group.)
. (You can just give the order of each group.)
- (ii)
- For each prime in (i), let
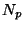 be the number of
points in the group. (Don't forget the point infinity.)
For the set of primes satisfying
be the number of
points in the group. (Don't forget the point infinity.)
For the set of primes satisfying
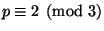 ,
can you see a pattern for the values of
,
can you see a pattern for the values of 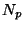 ?
Make a general conjecture for the value of
?
Make a general conjecture for the value of 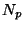 when
when
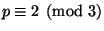 .
.
- (iii)
- Prove your conjecture.
- 4.
- (6 points)
Let
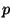 be a prime and let
be a prime and let 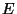 be the elliptic curve
defined by the equation
be the elliptic curve
defined by the equation
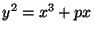 .
Use Lutz-Nagel to find all points of finite order in
.
Use Lutz-Nagel to find all points of finite order in
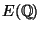 .
.
- 5.
- (4 points)
- (iv)
- Let
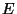 be an elliptic curve over the real numbers
be an elliptic curve over the real numbers
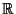 .
Prove that
.
Prove that
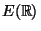 is not a finitely generated abelian group.
is not a finitely generated abelian group.
- (v)
- Let
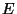 be an elliptic curve over a finite field
be an elliptic curve over a finite field
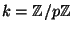 .
Prove that
.
Prove that 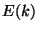 is a finitely generated abelian group.
is a finitely generated abelian group.



Next: About this document ...
William A Stein
2001-11-23
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001