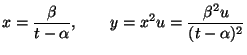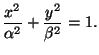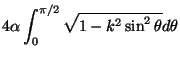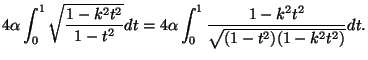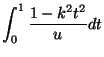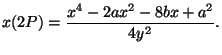Next: About this document ...
Homework 8: Elliptic Curves
DUE WEDNESDAY, NOVEMBER 21
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
There are six problems.
Some of the problems involve tedious
algebra, and in all such cases you are allowed to do that algebra
using, e.g., PARI as long as you explain
how you used the system to do the algebra.
Problems 4, 5, and 6 are from Silverman and Tate's
book Rational Points on Elliptic Curves.
- 1.
- (3 points) Consider the elliptic curve
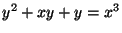 over
over
 .
Find a linear change of variables that transforms this curve into
a curve of the form
.
Find a linear change of variables that transforms this curve into
a curve of the form
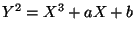 for rational numbers
for rational numbers 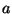 and
and 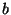 .
.
- 2.
- (6 points) Let
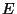 be the elliptic curve over the finite
field
be the elliptic curve over the finite
field
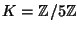 defined by the equation
defined by the equation
- (i)
- List all
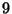 elements of
elements of 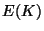 .
.
- (ii)
- What is the structure of the group
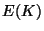 , as a product of cyclic groups?
, as a product of cyclic groups?
- 3.
- (8 points) Let
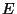 be an elliptic curve over
be an elliptic curve over
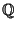 .
Define a binary operation
.
Define a binary operation  on
on 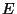 as follows:
Thus the
as follows:
Thus the  of
of 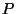 and
and 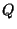 is the third
point of intersection of the line through
is the third
point of intersection of the line through 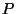 and
and 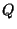 with
with 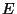 .
.
- (iii)
- Lists the axiom(s) of a group that fail for
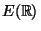 equipped with this binary operation.
(The group axioms are ``identity'', ``inverses'', and ``associativity''.)
equipped with this binary operation.
(The group axioms are ``identity'', ``inverses'', and ``associativity''.)
- (iv)
- Under
what conditions on
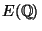 does this binary operation
define a group structure on
does this binary operation
define a group structure on
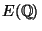 ? (E.g., when
? (E.g., when
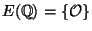 this binary operation does define a group.)
this binary operation does define a group.)
- 4.
- (6 points) Let
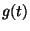 be a quartic polynomial with distinct (complex) roots,
and let
be a quartic polynomial with distinct (complex) roots,
and let 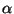 be a root of
be a root of 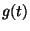 . Let
. Let
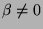 be any number.
be any number.
- (v)
- Prove that the equations
give an ``algebraic transformation'' between the curve
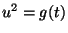 and the curve
and the curve 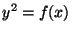 , where
, where 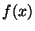 is the cubic polynomial
is the cubic polynomial
- (vi)
- Prove that if
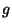 has distinct (complex) roots, then
has distinct (complex) roots, then 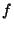 also
has distinct roots, and so
also
has distinct roots, and so
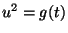 is an elliptic curve.
is an elliptic curve.
- 5.
- (8 points)
In this problem you will finally find out exactly
why elliptic curves are called ``elliptic curves''!
Let
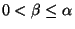 , and let
, and let 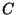 be the ellipse
be the ellipse
- (vii)
- Prove that the arc length of
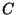 is given
by the integral
for an appropriate choice of constant
is given
by the integral
for an appropriate choice of constant 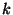 depending on
depending on 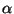 and
and 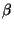 .
.
- (viii)
- Check your value for
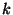 in (i) by verifying that when
in (i) by verifying that when
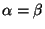 ,
the integral yields the correct value for the arc length of a circle.
,
the integral yields the correct value for the arc length of a circle.
- (ix)
- Prove that the integral in (i) is also equal to
- (x)
- Prove that if the ellipse
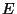 is not a circle, then the equation
defines an elliptic curve (cf. the previous exercise). Hence
the problem of determining the arc length of an ellipse comes down
to evaluating the integral
on the ``elliptic'' curve
is not a circle, then the equation
defines an elliptic curve (cf. the previous exercise). Hence
the problem of determining the arc length of an ellipse comes down
to evaluating the integral
on the ``elliptic'' curve
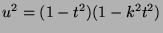 .
.
- 6.
- (8 points)
Suppose that
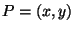 is a point on the cubic curve
is a point on the cubic curve
- (xi)
- Verify that the
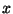 coordinate of the point
coordinate of the point 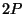 is given by the duplication formula
is given by the duplication formula
- (xii)
- Derive a similar formula for the
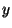 coordinate of
coordinate of 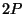 in terms of
in terms of 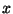 and
and 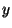 .
.
- (xiii)
- Find a polynomial in
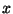 whose roots are the
whose roots are the 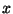 -coordinates
of the points
-coordinates
of the points 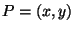 satisfying
satisfying
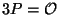 . [Hint: The
relation
. [Hint: The
relation
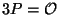 can also be written
can also be written 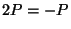 .]
.]
- (xiv)
- For the particular curve
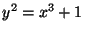 , solve the equation
in (iii) to find all of the points satisfying
, solve the equation
in (iii) to find all of the points satisfying
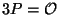 .
Note that you will have to use complex numbers.
.
Note that you will have to use complex numbers.



Next: About this document ...
William A Stein
2001-11-13
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001