


Next: About this document ...
A. Student
Math 124 Problem Set 7
1. D=-155 There are four elements:
![$ [[1, 1, 39],
[3, -1, 13], [3, 1, 13], [5, 5, 9]].$](img1.png)
By the structure
theorem,
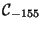 is isomorphic to either
is isomorphic to either 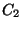 x
x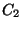 or
or 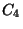 . It is easy to verify that
. It is easy to verify that ![$ [1,1,39]$](img5.png) is the identity.
From this we find that
is the identity.
From this we find that ![$ [3,-1,13]$](img6.png) has order 4, so it must be
that
has order 4, so it must be
that
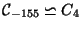 .
.
D=-231
There are twelve elements:
![$ [1, 1, 58], [2, -1, 29], [2, 1, 29],
[3, 3, 20], [4, -3, 15], [4, 3, 15], $](img8.png)
![$ [5, -3, 12], [5, 3, 12], [6, -3, 10], [6, 3, 10], [7,
7, 10], [8, 5, 8].$](img9.png) Therefore
Therefore
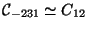 or
or 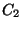 x
x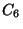 . The identity is
. The identity is ![$ [1,1,58]$](img12.png) . Both
. Both ![$ [2,-1,29]$](img13.png) and
and
![$ [2,1,29]$](img14.png) have order 6, which is impossible in
have order 6, which is impossible in 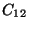 , so
, so
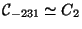 x
x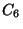 .
.
D=-660 There are eight elements:
![$ [1, 0, 165], [10, 10,
19], [11, 0, 15], [13, 4, 13], [2, 2, 83], [3, 0, 55], [5, 0,
33],$](img17.png)
![$ [6, 6, 29].$](img18.png) The first element is the identity,
and all others have order 2. Therefore
The first element is the identity,
and all others have order 2. Therefore
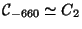 x
x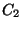 x
x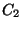 .
.
D=-12104 There are forty-eight elements: (listed in an
email from Professor Stein). By the structure theorem,
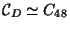 ,
, 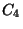 x
x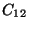 , or
, or 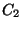 x
x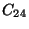 .
The identity element is
.
The identity element is
![$ [1,0,3026]$](img22.png) , and using it we find two
elements of order four:
, and using it we find two
elements of order four:
![$ [45,-26,71]$](img23.png) and
and
![$ [50,-36,67]$](img24.png) ,
eliminating everything but
,
eliminating everything but 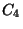 x
x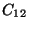 .
.
D=-10015 There are fifty-four elements (listed in an
email from Professor Stein). Therefore
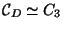 x
x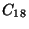 or
or 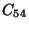 . The identity is
. The identity is
![$ [1,1,2504]$](img28.png) ; from
this we find two elements with order 9:
; from
this we find two elements with order 9:
![$ [10,-5,251]$](img29.png) and
and
![$ [10,5,251]$](img30.png) . Therefore the group cannot be
. Therefore the group cannot be 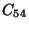 , so
, so
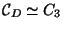 x
x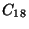 .
.
2. The three graphs are on the next page, plotted in
MAPLE.
3. Differentiating implicitly, the slope of the tangent
at 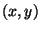 is
is
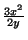 . At
. At 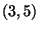 , the slope is
, the slope is
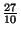 , and the tangent line has equation
, and the tangent line has equation
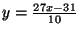 . Substituting into the relation
. Substituting into the relation
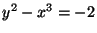 , we have
, we have
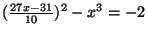 , which
simplifies to the polynomial
, which
simplifies to the polynomial
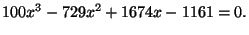
This
polynomial has a double root at 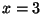 , so it factors into
, so it factors into
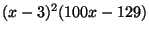 , giving a rational root with
, giving a rational root with 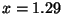 .
Therefore
.
Therefore
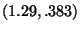 is a rational solution to the original
equation.
is a rational solution to the original
equation.



Next: About this document ...
William A Stein
2001-12-10