


Next: About this document ...
Homework 2: Congruences
DUE WEDNESDAY, OCTOBER 3.
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
Do not use a computer for problems 2-8, except for basic arithmetic
and to check your work (these problems are easy to solve in PARI).
Remember to work in groups and cite sources of help.
- Find complete sets of residues modulo
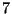 , all of whose elements
are (a) nonnegative, (b) odd, (c) even, (d) prime.
, all of whose elements
are (a) nonnegative, (b) odd, (c) even, (d) prime.
- Find an integer
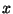 such that
such that
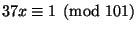 .
.
- What is the order of
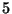 modulo
modulo 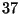 ?
?
- Let
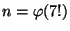 . Compute the prime factorization of
. Compute the prime factorization of 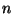 .
.
- Find
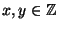 such that
such that
- Find an
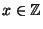 such that
such that
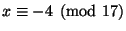 and
and
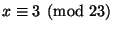 .
.
- Compute
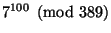 .
.
- Find a number
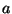 such that
such that
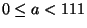 and
(See Problem 2.05 on page 217 of Davenport.)
and
(See Problem 2.05 on page 217 of Davenport.)
- Prove that if
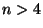 is composite then
is composite then
- For what values of
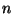 is
is
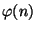 odd?
odd?
- Find your own
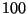 -digit number
-digit number 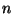 such that
such that
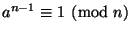 for
for 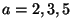 .
.
- Seven thieves try to share a hoard of gold bars equally between
themselves. Unfortunately, six bars are left over, and in the fight
over them, one thief is killed. The remaining six thieves, still
unable to share the bars equally since two are left over, again fight,
and another is killed. When the remaining five share the bars, one
bar is left over, and it is only after yet another thief is killed
that an equal sharing is possible. What is the minimum number of bars
which allows this to happen?
- An elderly woman goes to a market where a horse tramples her basket
crushing her eggs. The horse's honest rider offers to pay for the
damages and asks her how many eggs she had brought. She doesn't
remember the exact number, but recalls that when she had taken them
out two at a time, there was one egg left. The same happened when she
picked them out three, four, five, and six at a time, but when she
took them out seven at a time two were left. What is the smallest
number of eggs she could have had?



Next: About this document ...
William A Stein
2001-10-01
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001