Elliptic Curves Over the Rational Numbers
Figure 6.5:
Louis J. Mordell
|
|
Let 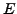 be an elliptic curve defined over
be an elliptic curve defined over
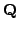 . The following
is a deep theorem about the group
. The following
is a deep theorem about the group
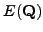 .
.
Mordell's theorem implies that it makes sense to ask whether or not we
can compute
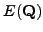 , where by ``compute'' we mean find a finite set
, where by ``compute'' we mean find a finite set
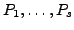 of points on
of points on 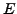 that generate
that generate
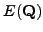 as an abelian
group. There is a systematic approach to computing
as an abelian
group. There is a systematic approach to computing
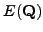 called
``descent'' (see e.g., [#!cremona:algs!#,#!mwrank!#,#!silverman:aec!#]).
It is widely believed that the method of descent will always succeed,
but nobody has yet proved that it will. Proving that descent works
for all curves is one of the central open problem in number theory,
and is closely related to the Birch and Swinnerton-Dyer conjecture
(one of the Clay Math Institute's million dollar prize problems). The
crucial difficulty amounts to deciding whether or not certain
explicitly given curves have any rational points on them or not (these
are curves that have points over
called
``descent'' (see e.g., [#!cremona:algs!#,#!mwrank!#,#!silverman:aec!#]).
It is widely believed that the method of descent will always succeed,
but nobody has yet proved that it will. Proving that descent works
for all curves is one of the central open problem in number theory,
and is closely related to the Birch and Swinnerton-Dyer conjecture
(one of the Clay Math Institute's million dollar prize problems). The
crucial difficulty amounts to deciding whether or not certain
explicitly given curves have any rational points on them or not (these
are curves that have points over
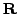 and modulo
and modulo 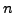 for all
for all 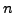 ).
).
The details of using descent to computing
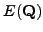 are beyond
the scope of this book. In several places below we will simply assert
that
are beyond
the scope of this book. In several places below we will simply assert
that
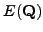 has a certain structure or is generated by certain
elements. In each case, we computed
has a certain structure or is generated by certain
elements. In each case, we computed
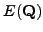 using a computer
implementation of this method.
using a computer
implementation of this method.
Subsections
William
2007-06-01
![]() are beyond
the scope of this book. In several places below we will simply assert
that
are beyond
the scope of this book. In several places below we will simply assert
that
![]() has a certain structure or is generated by certain
elements. In each case, we computed
has a certain structure or is generated by certain
elements. In each case, we computed
![]() using a computer
implementation of this method.
using a computer
implementation of this method.