The Sequence of Prime Numbers
This section is concerned with three questions:
- Are there infinitely many primes?
- Given
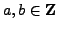 ,
are there infinitely many primes of the form
,
are there infinitely many primes of the form 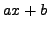 ?
?
- How are the primes spaced along the number line?
We first show that there are infinitely
many primes, then state Dirichlet's theorem
that if
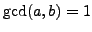 ,
then
,
then 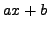 is a prime for infinitely many values of
is a prime for infinitely many values of 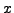 . Finally, we
discuss the Prime Number Theorem
which asserts that there are
asymptotically
. Finally, we
discuss the Prime Number Theorem
which asserts that there are
asymptotically 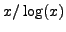 primes less than
primes less than 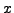 ,
and we make a connection between this asymptotic formula
and the Riemann Hypothesis.
,
and we make a connection between this asymptotic formula
and the Riemann Hypothesis.
Subsections
William
2007-06-01