Let 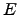 be an elliptic curve defined over
be an elliptic curve defined over 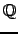 with conductor
with conductor 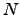 ,
and fix a modular parametrization
,
and fix a modular parametrization
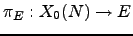 .
.
Let 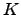 be a quadratic imaginary field such that the primes dividing
be a quadratic imaginary field such that the primes dividing
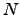 are all unramified and split in
are all unramified and split in 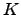 . For simplicity, we will also
assume that
. For simplicity, we will also
assume that
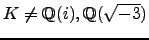 . Let
. Let 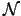 be an integral
ideal of
be an integral
ideal of 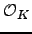 such that
such that
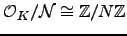 .
Then
.
Then
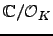 and
and
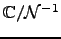 define two elliptic curves
over
define two elliptic curves
over 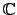 , and since
, and since
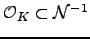 , there is
a natural map
, there is
a natural map
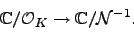 |
(3.2.1) |
By Proposition 3.3 the kernel of this map
is
Exercise 3.19
Prove that there is an isomorphism
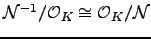
of finite abelian group.
The modular curve 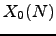 parametrizes isomorphism
classes of pairs
parametrizes isomorphism
classes of pairs 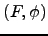 , where
, where 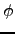 is an isogeny
with kernel cyclic of order
is an isogeny
with kernel cyclic of order 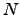 . Thus
. Thus
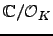 and the isogeny (3.2.1) define an element
and the isogeny (3.2.1) define an element
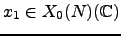 . The discussion of Section 3.1.3
along with properties of modular curves proves the following
proposition.
. The discussion of Section 3.1.3
along with properties of modular curves proves the following
proposition.
Proposition 3.20
We have
where 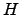 is the Hilbert class field of
is the Hilbert class field of 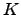 .
.
Definition 3.21 (Heegner point)
The
Heegner point associated to
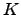
is
More generally, for any integer 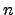 , let
, let
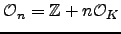 be the order in
be the order in 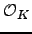 of
index
of
index 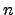 . Then
. Then
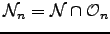 satisfies
satisfies
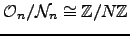 , and the pair
, and the pair
defines a point
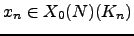 ,
where
,
where 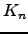 is the ray class field of
conductor
is the ray class field of
conductor 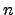 over
over 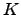 .
.
Definition 3.22 (Heegner point of conductor
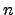
)
The Heegner point of conductor
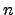
is
William
2007-05-25
![]() be a quadratic imaginary field such that the primes dividing
be a quadratic imaginary field such that the primes dividing
![]() are all unramified and split in
are all unramified and split in ![]() . For simplicity, we will also
assume that
. For simplicity, we will also
assume that
![]() . Let
. Let ![]() be an integral
ideal of
be an integral
ideal of ![]() such that
such that
![]() .
Then
.
Then
![]() and
and
![]() define two elliptic curves
over
define two elliptic curves
over ![]() , and since
, and since
![]() , there is
a natural map
, there is
a natural map
![]() , let
, let
![]() be the order in
be the order in ![]() of
index
of
index ![]() . Then
. Then
![]() satisfies
satisfies
![]() , and the pair
, and the pair