Next: Example: A Curve of Up: The Birch and Swinnerton-Dyer Previous: Example: A Rank 4 Contents Index
In Chapter 1 (see Theorem 1.15)
we defined a ![]() -adic
-adic ![]() -series
-series
First, suppose
![]() , i.e.,
, i.e.,
![]() . Recall that the interpolation property
(1.5.1) for
. Recall that the interpolation property
(1.5.1) for
![]() implies that
implies that
Notice in (2.5.2) that since ![]() has rank
has rank ![]() , we have
, we have
![]() , so there is no issue with the left hand side
being a
, so there is no issue with the left hand side
being a ![]() -adic number and the right hand side not making sense.
It would be natural to try to generalize (2.5.2) to higher order
of vanishing as follows. Let
-adic number and the right hand side not making sense.
It would be natural to try to generalize (2.5.2) to higher order
of vanishing as follows. Let
![]() denote the leading
coefficient of the power series
denote the leading
coefficient of the power series
![]() . Then
. Then
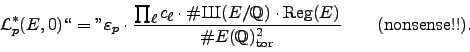 |
(2.5.3) |
The key new idea needed to make
a conjecture is to replace the real-number regulator
![]() with a
with a ![]() -adic regulator
-adic regulator
![]() .
This new regulator is defined in a way analogous to the classical
regulator, but where many classical complex analytic objects
are replaced by
.
This new regulator is defined in a way analogous to the classical
regulator, but where many classical complex analytic objects
are replaced by ![]() -adic analogues. Moreover, the
-adic analogues. Moreover, the ![]() -adic regulator
was, until recently (see [MST06]), much
more difficult to compute than the classical real regulator.
We will define the
-adic regulator
was, until recently (see [MST06]), much
more difficult to compute than the classical real regulator.
We will define the ![]() -adic number
-adic number
![]() in the next section.
in the next section.
Let ![]() be an elliptic curve over
be an elliptic curve over ![]() and let
and let ![]() be a prime of
good ordinary reduction for
be a prime of
good ordinary reduction for ![]() . Then the rank of
. Then the rank of ![]() equals
equals
![]() and
and
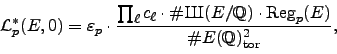 |
(2.5.4) |