Next: The inf-res Sequence Up: Galois Cohomology Previous: Galois Cohomology Contents Index
Let ![]() be the submodule of elements of
be the submodule of elements of ![]() that are fixed by
that are fixed by ![]() .
Notice that if
.
Notice that if ![]() is a homomorphism of
is a homomorphism of ![]() -modules, then
restriction defines a homomorphism
-modules, then
restriction defines a homomorphism ![]() , so
, so ![]() is a functor. In fact, it is a left-exact functor:
is a functor. In fact, it is a left-exact functor:
We construct ![]() explicitly as follows.
Consider
explicitly as follows.
Consider ![]() as a
as a ![]() -module, equipped with the
trivial
-module, equipped with the
trivial ![]() -action.
Consider the following free resolution of
-action.
Consider the following free resolution of ![]() .
Let
.
Let ![]() be the free
be the free ![]() -module with basis
the set of
-module with basis
the set of ![]() tuples
tuples
![]() , and
with
, and
with ![]() acting on
acting on ![]() componentwise:
componentwise:
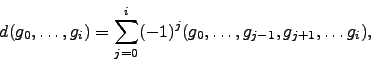
The cohomology groups ![]() are then
the cohomology groups of the complex
are then
the cohomology groups of the complex
![]() .
We identify an element of
.
We identify an element of ![]() with a function
with a function
![]() such that the condition
such that the condition
The boundary map
![]() on such functions
on such functions
![]() is then given explicitly by the formula
is then given explicitly by the formula
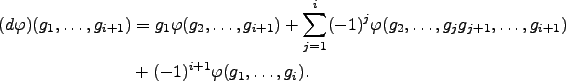
The group of
![]() -cocycles is the group of
-cocycles is the group of
![]() ,
as above are functions of
,
as above are functions of ![]() variables such that
variables such that
![]() .
The subgroup of
.
The subgroup of ![]() -coboundaries
is the image of
-coboundaries
is the image of ![]() under
under ![]() .
Explicitly, the cohomology group
.
Explicitly, the cohomology group ![]() is
the quotient of the group group of
is
the quotient of the group group of ![]() -cocycles
modulo the subgroup of
-cocycles
modulo the subgroup of ![]() -coboundaries.
-coboundaries.
When ![]() , the
, the ![]() -cocycles
are the maps
-cocycles
are the maps ![]() such that
such that
William 2007-05-25