Next: How Many Letters Can
Up: Lecture 9: The RSA
Previous: How Nikita Decrypts a
Contents
Encoding a Phrase in a Number
Think of a sequence of letters and spaces as a number in base 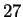 .
Let a single-space correspond to 0, the letter
.
Let a single-space correspond to 0, the letter 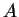 to 1,
to 1, 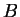 to 2,
...,
to 2,
..., 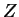 to 26. Thus, e.g., ``HARVARD'' denotes a number written in
base
to 26. Thus, e.g., ``HARVARD'' denotes a number written in
base 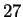 . The corresponding number written in decimal is
. The corresponding number written in decimal is
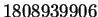 :
:
HARVARD
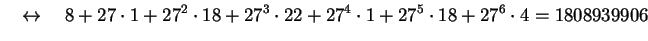
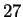 :
and so on.
:
and so on.
Subsections
William A Stein
2001-10-01