



Next: Sending Nikita an Encrypted
Up: How RSA works
Previous: One-way Functions
Contents
Here is how Nikita makes a one-way function 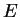 :
:
- Nikita picks two large primes
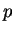 and
and 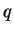 , and lets
, and lets 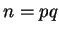 .
.
- It is easy for Nikita to then compute
- Nikita next chooses a ``random'' integer
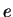 with
with
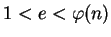
and
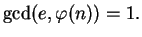
- Finally, Nikita uses the algorithm from Lecture 7 to find a
solution
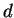 to the equation
to the equation
The Encoding Function:
Nikita defines a function
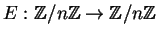
(Recall that
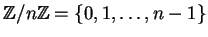 with addition and multiplication
modulo
with addition and multiplication
modulo 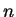 .)
Then anybody can compute
.)
Then anybody can compute 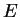 fairly quickly using the repeated-squaring
algorithm from Lecture 7.
fairly quickly using the repeated-squaring
algorithm from Lecture 7.
Nikita's public key is the pair of integers 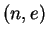 , which is
just enough information for people to easily compute
, which is
just enough information for people to easily compute 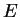 .
Nikita knows a number
.
Nikita knows a number 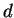 such that
such that
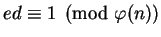 ,
so, as we will see below, she can quickly compute
,
so, as we will see below, she can quickly compute 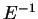 .
.
Now Michael or even The Collective can send Nikita a message whenever
they want, even if Nikita is asleep. They look up how to compute 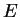 and compute
and compute
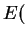 their message
their message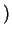 .
.




Next: Sending Nikita an Encrypted
Up: How RSA works
Previous: One-way Functions
Contents
William A Stein
2001-10-01
![]()
![]() , which is
just enough information for people to easily compute
, which is
just enough information for people to easily compute ![]() .
Nikita knows a number
.
Nikita knows a number ![]() such that
such that
![]() ,
so, as we will see below, she can quickly compute
,
so, as we will see below, she can quickly compute ![]() .
.
![]() and compute
and compute
![]() their message
their message![]() .
.