



Next: A Bigger Example in
Up: Examples
Previous: Examples
Contents
So the arithmetic is easy to follow, we use small primes 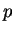 and
and 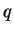 and encrypt the single letter ``X''.
and encrypt the single letter ``X''.
- Choose
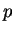 and
and 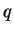 : Let
: Let 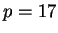 ,
, 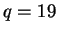 , so
, so
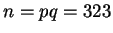 .
.
- Compute
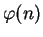 :
:
- Randomly choose an
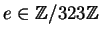 : We choose
: We choose 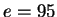 .
.
- Solve
Using the GCD algorithm, we find that
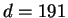 solves
the equation.
solves
the equation.
The public key is 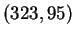 . So
. So
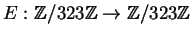 is
defined by
is
defined by
Next, we encrypt the letter ``X''. It is encoded as the number
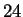 , since X is the
, since X is the 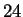 th letter of the alphabet.
We have
th letter of the alphabet.
We have
To decrypt, we compute 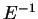 :
:
William A Stein
2001-10-01
![]() . So
. So
![]() is
defined by
is
defined by
![]() , since X is the
, since X is the ![]() th letter of the alphabet.
We have
th letter of the alphabet.
We have
![]() :
: