How to Compute $a^m\pmod{n}$ Efficiently

As we will see on Friday, a quick method to compute $a^m\pmod{n}$ is absolutely essential to public-key cryptography.

Naive Algorithm: Compute $a\cdot a \cdot \cdots \cdot a\pmod{n}$ by repeatedly multiplying by $a$ and reducing modulo $m$. This is BAD because it takes $m-1$ multiplications.

Clever Algorithm: The following observation is the key idea which makes the clever algorithm work. Write $m=\sum_{i=1}^r \varepsilon _i 2^i$ with each $\varepsilon _i\in\{0,1\}$, i.e., write $m$ in base $2$ (binary). Then

$$a^m = \prod_{\varepsilon _i = 1} a^{2^i}\pmod{n}.$$

It is straightforward to write a number $m$ in binary, as follows: If $m$ is odd, then $\varepsilon _0=1$, otherwise $\varepsilon _0=0$. Replace $m$ by floor$({\frac{m}{2}})$. If the new $m$ is odd then $\varepsilon _1=1$, otherwise $\varepsilon _1=0$. Keep repeating until $m=0$.

Example 2.1  


Problem: Compute the last $2$ digits of $6^{91}$.


Solution: We compute $6^{91}\pmod{100}$.

$i$	$m$	$\varepsilon _i$	$6^{2^i}$ mod 100
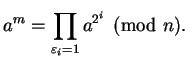
0	91	1	6
1	45	1	36
2	22	0	96
3	11	1	16
4	5	1	56
5	2	0	36
6	1	1	96

As a check, note that $91 = 1011011_2 = 2^6+2^4+2^3+2+2^0$. Finally, we have

$$6^{91} = 6^{2^6}\cdot 6^{2^4} \cdot 6^{2^3}\cdot 6^2 \cdot 6 \equiv 96 \cdot 56 \cdot 16 \cdot 36 \cdot 6 \equiv 56\pmod{100}.$$

Summary of above table: The first column, labeled $i$, is just to keep track of $i$. The second column, labeled $m$, is got by dividing the entry above it by $2$ and taking the integer part of the result. The third column, labeled $\varepsilon _i$, simply records whether or not the second column is odd. The forth column is computed by squaring, modulo 100, the entry above it.

Some examples in PARI to convince you that powering isn't too difficult:

? Mod(17,389)^5000
%13 = Mod(330, 389)
? Mod(2903,49084098)^498494
%14 = Mod(13189243, 49084098)

These both take no noticeable time.