


Next: To solve
Up: How to Solve
Previous: How to Solve
Proposition 1.1
Suppose
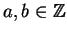
and
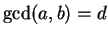
. Then
there exists
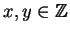
such that
I won't give a formal proof of this proposition, though there
are many in the literature. Instead I will show you how to
find 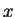 and
and 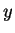 in practice, because that's what you will
need to do in order to solve equations like
in practice, because that's what you will
need to do in order to solve equations like
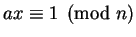 .
.
Example 1.2
Let
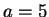
and
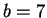
.
The steps of the Euclidean
algorithm are:
On the right, we have written each partial remainder as a
linear combination of
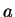
and
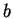
. In the last step, we write
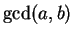
as a linear combination of
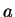
and
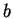
, as desired.
That example wasn't too complicated, next we try a much longer example.
Example 1.3
Let
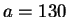
and
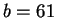
. We have
Thus
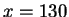
and
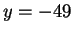
.
Remark 1.4
For our present purposes it will always be sufficient to find one
solution to
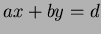
. In fact, there are always
infinitely many solutions. If
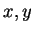
is a solution to
then for any
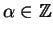
,
is also a solution, and all
solutions are of the above form for some
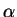
.
It is also possible to compute 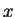 and
and 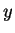 using PARI.
using PARI.
? ?bezout
bezout(x,y): gives a 3-dimensional row vector [u,v,d] such that
d=gcd(x,y) and u*x+v*y=d.
? bezout(130,61)
%1 = [23, -49, 1]



Next: To solve
Up: How to Solve
Previous: How to Solve
William A Stein
2001-09-25
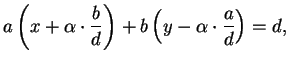
![]() and
and ![]() using PARI.
using PARI.