The discriminant ![]() of
of ![]() is congruent
to either 0 or
is congruent
to either 0 or ![]() modulo
modulo ![]() . Suppose
. Suppose ![]() is a negative discrimant
and consider the set of equivalence classes of binary quadratic forms
of discriminant
is a negative discrimant
and consider the set of equivalence classes of binary quadratic forms
of discriminant ![]() , where two forms
, where two forms ![]() and
and ![]() are equivalent if and only if there exists
are equivalent if and only if there exists
![]() such that
such that
![]() where
where
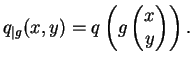
A reduced binary quadratic form is one for which
![]() and, in addition, when one of the two inequalities is an equality
then
and, in addition, when one of the two inequalities is an equality
then ![]() . Every form is equivalent to exactly one reduced
form, so it is possible to decide whether or not two forms
are equivalent. Also, there are only finitely many equivalence
classes of fixed discriminant
. Every form is equivalent to exactly one reduced
form, so it is possible to decide whether or not two forms
are equivalent. Also, there are only finitely many equivalence
classes of fixed discriminant ![]() . This finite set has a
natural group structure.
. This finite set has a
natural group structure.