


Next: About this document ...
Lecture 34: The Birch and Swinnerton-Dyer Conjecture, Part 1
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
The next three lectures will be about the
Birch and Swinnerton-Dyer conjecture, which is
considered by many people to be the most important
accessible open problem in number theory. Today I
will guide you through Wiles's Clay Math Institute
paper on the Birch and Swinnerton-Dyer conjecture.
On Friday, I will talk about the following open problem, which is a
frustrating specific case of the Birch and Swinnerton-Dyer conjecture.
Let 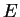 be the elliptic curve defined by
be the elliptic curve defined by
Denote by
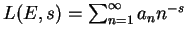 the corresponding
the corresponding 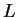 -series, which extends to a function
everywhere. The graph of
-series, which extends to a function
everywhere. The graph of 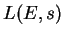 for
for
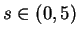 is
given on the next page.
It can be proved that
is
given on the next page.
It can be proved that
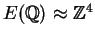 by showing that
by showing that
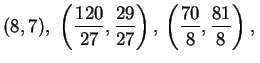
and
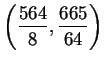
generate a ``subgroup of finite index'' in
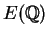 .
The Birch and Swinnerton-Dyer Conjecture then predicts that
which looks plausible from the shape of the graph on the next page.
It is relatively easy to prove that
the following is equivalent to showing that
.
The Birch and Swinnerton-Dyer Conjecture then predicts that
which looks plausible from the shape of the graph on the next page.
It is relatively easy to prove that
the following is equivalent to showing that
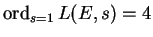 :
:
Open Problem:
Prove that
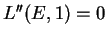 .
.
If you could solve this open problem, people like Gross, Tate, Mazur,
Zagier, Wiles, me, etc., would be very excited. The related
problem of giving an example of an 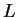 -series with
-series with
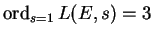 , was solved as a consequence of a very deep
theorem of Gross and Zagier, and resulting in an effective solution to
Gauss's class number problem.
, was solved as a consequence of a very deep
theorem of Gross and Zagier, and resulting in an effective solution to
Gauss's class number problem.
John Tate gave a talk about the BSD conjecture for the Clay Math
Institute. I strongly encourage you to watch it online at
http://www.msri.org/publications/ln/hosted/cmi/2000/cmiparis/index-tate.html
|
unit=.9in
(-0.5,-2)(5,2)
[gridcolor=lightgray]
[linewidth=0.03]->(-0.5,0)(5,0)(5.2,0)
[linewidth=0.03]->(0,-2)(0,2)(0.1,2.25)
[linecolor=red](1,0)0.06
[linecolor=blue]
(0,0)
(0.009999999999999999999999999999,20.17460740732031218029067105)
(0.01999999999999999999999999999,36.49248092043218759414227962)
(0.02999999999999999999999999999,49.48695269194186255570395989)
(0.03999999999999999999999999999,59.62809499064306722407223772)
(0.04999999999999999999999999999,67.32949817701725860474850393)
(0.05999999999999999999999999999,72.95437998695321784902246547)
(0.06999999999999999999999999999,76.82108703674534698230608976)
(0.07999999999999999999999999999,79.20804440435897043647662713)
(0.08999999999999999999999999999,80.35820445115398146915461672)
(0.09999999999999999999999999999,80.48304170441465810207415387)
(0.1099999999999999999999999999,79.76613660406133174625793745)
(0.1199999999999999999999999999,78.36638720713565471334218075)
(0.1299999999999999999999999999,76.42088452189766469084520681)
(0.1399999999999999999999999999,74.04748399111477869470341911)
(0.1499999999999999999999999999,71.34710274352131875238762686)
(0.1599999999999999999999999999,68.40576956639155116679637679)
(0.1699999999999999999999999999,65.29645210439220133457469776)
(0.1799999999999999999999999999,62.08068354485849675320142694)
(0.1899999999999999999999999999,58.81000899267982264641223734)
(0.1999999999999999999999999999,55.52726985520684582203751378)
(0.2099999999999999999999999999,52.26774283592287994132381501)
(0.2199999999999999999999999999,49.06014856276556567828076763)
(0.2299999999999999999999999999,45.92754344141284383534396879)
(0.2399999999999999999999999999,42.88810701477216095300037175)
(0.2500000000000000000000000000,39.95583591725886436605311523)
(0.2599999999999999999999999999,37.14115442682657456540803882)
(0.2699999999999999999999999999,34.45145063037828623093305962)
(0.2799999999999999999999999999,31.89154632102089971062111326)
(0.2899999999999999999999999999,29.46410793109383578525135981)
(0.2999999999999999999999999999,27.17000506602518061597947147)
(0.3099999999999999999999999999,25.00862253439015019890448691)
(0.3199999999999999999999999999,22.97813116310177967557620869)
(0.3299999999999999999999999999,21.07572213794885965683462997)
(0.3399999999999999999999999999,19.29780911363895258131960784)
(0.3499999999999999999999999999,17.64020188943555017633327563)
(0.3599999999999999999999999999,16.09825504210457925139305818)
(0.3699999999999999999999999999,14.66699454326279499576807542)
(0.3799999999999999999999999999,13.34122505973041656327517788)
(0.3899999999999999999999999999,12.11562033981553963057313496)
(0.3999999999999999999999999999,10.98479882256070828538534132)
(0.4099999999999999999999999999,9.943386368083383947466728763)
(0.4199999999999999999999999999,8.986067792701650934369969225)
(0.4299999999999999999999999999,8.107628700234563525818535593)
(0.4399999999999999999999999999,7.302988928586518979021916724)
(0.4499999999999999999999999999,6.567228776537510403916594514)
(0.4599999999999999999999999999,5.895609037808749758128609910)
(0.4699999999999999999999999999,5.283585746356747623589733925)
(0.4799999999999999999999999999,4.726820427014403603207828295)
(0.4899999999999999999999999999,4.221186547723964451899689776)
(0.5000000000000000000000000000,3.762772782494687754526881867)
(0.5099999999999999999999999999,3.347883616780079475458459212)
(0.5199999999999999999999999999,2.973037758219996513199228676)
(0.5299999999999999999999999999,2.634964754739207607589602182)
(0.5399999999999999999999999999,2.330600168028682449712596851)
(0.5499999999999999999999999999,2.057079602728938881782014276)
(0.5599999999999999999999999999,1.811731849526851974888215643)
(0.5699999999999999999999999999,1.592071363273333449258930595)
(0.5799999999999999999999999999,1.395790264592613793193107804)
(0.5899999999999999999999999999,1.220750024801029588629612509)
(0.5999999999999999999999999999,1.064972968849014570738009102)
(0.6099999999999999999999999999,0.9266337090529745829497283098)
(0.6199999999999999999999999999,0.8040506032421436529502188197)
(0.6299999999999999999999999999,0.6956773142935737278953165664)
(0.6399999999999999999999999999,0.6000945335828484520729664871)
(0.6499999999999999999999999999,0.5160019183851058048608615062)
(0.6599999999999999999999999999,0.4422102824932734723852967661)
(0.6699999999999999999999999999,0.3776340700748442896394133312)
(0.6799999999999999999999999999,0.3212841348834891250179487532)
(0.6899999999999999999999999999,0.2722608402152899327179309314)
(0.6999999999999999999999999999,0.2297474893069316371408115573)
(0.7099999999999999999999999999,0.1930040910861989698630156271)
(0.7199999999999999999999999999,0.1613614621891930253258516617)
(0.7299999999999999999999999999,0.1342156628522034383917738953)
(0.7399999999999999999999999999,0.1110227615790083457114122966)
(0.7500000000000000000000000000,0.09129392129667414518098480549)
(0.7599999999999999999999999999,0.07459079797405312211187159854)
(0.7699999999999999999999999999,0.06052124132473794610248824865)
(0.7799999999999999999999999999,0.04873528619520886474474134312)
(0.7899999999999999999999999999,0.03892142250086749266271155850)
(0.7999999999999999999999999999,0.03080313107503010887527356618)
(0.8099999999999999999999999999,0.02413567250142808775689375590)
(0.8199999999999999999999999999,0.01870311587666825308627117243)
(0.8299999999999999999999999999,0.01431559446691944601678069902)
(0.8399999999999999999999999999,0.01080677535797030118779995171)
(0.8499999999999999999999999999,0.008031530428166537313088826674)
(0.8599999999999999999999999999,0.005863796280892651616045409318)
(0.8699999999999999999999999999,0.004194611141076388195622582279)
(0.8799999999999999999999999999,0.002930317134784240786576375213)
(0.8899999999999999999999999999,0.001990916820450637832948807979)
(0.8999999999999999999999999999,0.001308573314500336314393575834)
(0.9099999999999999999999999999,0.0008262438444779515009749122133)
(0.9199999999999999999999999999,0.0004964370620328922663686765112)
(0.9299999999999999999999999999,0.0002800849501432968528544120962)
(0.9399999999999999999999999999,0.0001455206587485309187589983425)
(0.9499999999999999999999999999,0.00006755409634153535113332324454)
(0.9599999999999999999999999999,0.00002663758867231954273129854073)
(0.9699999999999999999999999999,0.000008114386827604695137558360759)
(0.9799999999999999999999999999,0.000001543263454951985960816259945)
(0.9899999999999999999999999999,0.00000009287616753530200698777679283)
(1.000000000000000000000000000,0)
(1.009999999999999999999999999,0.00000008613535242271793720817881641)
(1.019999999999999999999999999,0.000001327383632453574056960242273)
(1.029999999999999999999999999,0.000006472849519208711184577737210)
(1.039999999999999999999999999,0.00001970717637751214949546526075)
(1.049999999999999999999999999,0.00004635314997888051879883070784)
(1.059999999999999999999999999,0.00009261061561523324548962036876)
(1.069999999999999999999999999,0.0001653282453215230156051138830)
(1.079999999999999999999999999,0.0002718049657487095079831033217)
(1.089999999999999999999999999,0.0004196181138178058712824946368)
(1.099999999999999999999999999,0.0006164756272648974614962677827)
(1.099999999999999999999999999,0.0006164756272648974614962677827)
(1.199999999999999999999999999,0.006870279746547869692524606156)
(1.299999999999999999999999999,0.02451425929226668848552443352)
(1.399999999999999999999999999,0.05530486595233524676133790522)
(1.500000000000000000000000000,0.09765544070412340678441505311)
(1.599999999999999999999999999,0.1484133662890015288766060733)
(1.699999999999999999999999999,0.2041828834745631596498302481)
(1.799999999999999999999999999,0.2620135130277175192931976650)
(1.899999999999999999999999999,0.3196398583984175776395640284)
(2.000000000000000000000000000,0.3754772776917356690282702906)
(2.142857142857142857142857142,0.4502313491226790796900981145)
(2.285714285714285714285714285,0.5178521605298004955131946576)
(2.428571428571428571428571428,0.5779802204499079942278058454)
(2.571428571428571428571428571,0.6308850124153752579541337641)
(2.714285714285714285714285714,0.6771425457165369193256163032)
(2.857142857142857142857142857,0.7174458390192943996234368404)
(3.000000000000000000000000000,0.7525010360986485727517631927)
(3.142857142857142857142857142,0.7829749879942698159458508626)
(3.285714285714285714285714285,0.8094722550337551220911958042)
(3.428571428571428571428571428,0.8325281629388328047823509839)
(3.571428571428571428571428571,0.8526101345199758064458287717)
(3.714285714285714285714285714,0.8701229137173289116087300433)
(3.857142857142857142857142857,0.8854152900121340605812737059)
(4.000000000000000000000000000,0.8987870701281932147462079378)
(4.142857142857142857142857142,0.9104956815780882370859628481)
(4.285714285714285714285714285,0.9207621415644603190499847130)
(4.428571428571428571428571428,0.9297763100393346042082318535)
(4.571428571428571428571428571,0.9377014395533425632455706355)
(4.714285714285714285714285714,0.9446780780755271456938317299)
(4.857142857142857142857142857,0.9508273974961405102958036830)
(5.000000000000000000000000000,0.9562540230526573686678401977)
The
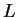
-series of the ``simplest'' known elliptic curve of rank
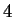
.



Next: About this document ...
William A Stein
2001-12-05
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001![]() be the elliptic curve defined by
be the elliptic curve defined by
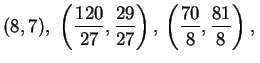 and
and 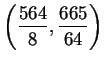
![]() .
.
![]() -series with
-series with
![]() , was solved as a consequence of a very deep
theorem of Gross and Zagier, and resulting in an effective solution to
Gauss's class number problem.
, was solved as a consequence of a very deep
theorem of Gross and Zagier, and resulting in an effective solution to
Gauss's class number problem.