LetWhenbe an irreducible polynomial in two variables over
. Find all rational numbers
such that

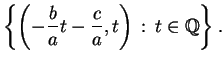
When ![]() is quadratic, the solution is not completely trivial, but it
is well understood. In this case, the equation
is quadratic, the solution is not completely trivial, but it
is well understood. In this case, the equation ![]() has infinitely
many rational solutions if and only if it has at least one solution.
Moreover, it is easy to describe all solutions when there is one. If
has infinitely
many rational solutions if and only if it has at least one solution.
Moreover, it is easy to describe all solutions when there is one. If
![]() is a solution and
is a solution and ![]() is a non-tangent line through
is a non-tangent line through
![]() , then
, then ![]() will intersect the curve
will intersect the curve ![]() in exactly one
other point
in exactly one
other point
![]() . Also
. Also
![]() since a quadratic
polynomial over
since a quadratic
polynomial over
![]() with
with ![]() rational root has both roots rational.
Thus the rational points on
rational root has both roots rational.
Thus the rational points on ![]() are in bijection with the slopes of
lines through
are in bijection with the slopes of
lines through ![]() .
.
Chapter 2 of [Kato et al.] is about how to decide whether
or not an ![]() of degree
of degree ![]() has a rational point. The answer is that
has a rational point. The answer is that
![]() has a rational solution if and only if
has a rational solution if and only if ![]() has a solution with
has a solution with
![]() and a solution with
and a solution with
![]() for every
``
for every
``![]() -adic field''
-adic field''
![]() . This condition, though it might sound
foreboding, is easy to check in practice. I encourage you to
flip through chapter 2 of loc. cit.
. This condition, though it might sound
foreboding, is easy to check in practice. I encourage you to
flip through chapter 2 of loc. cit.