


Next: Euclid's Algorithm for Computing
Up: Lecture 2: Prime Factorization
Previous: Prime Numbers
Let 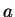 and
and 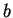 be two integers. The greatest common divisor
of
be two integers. The greatest common divisor
of 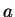 and
and 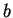 is the biggest number that divides both of them.
We denote it by ``
is the biggest number that divides both of them.
We denote it by ``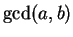 ''. Thus,
''. Thus,
Definition 2.1
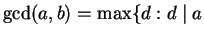
and
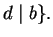
Warning: We define
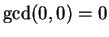 , instead of ``infinity''.
, instead of ``infinity''.
Here are a few gcd's:
Warning: In Davenport's book, he denotes our 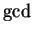 by HCF and calls it
the ``highest common factor''. I will use the notation
by HCF and calls it
the ``highest common factor''. I will use the notation 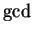 because
it is much more common.
because
it is much more common.
Subsections
William A Stein
2001-09-14
![]() by HCF and calls it
the ``highest common factor''. I will use the notation
by HCF and calls it
the ``highest common factor''. I will use the notation ![]() because
it is much more common.
because
it is much more common.