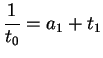
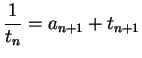
![$\displaystyle \frac{8}{3} = [2,1,2],$](img28.png)
![$\displaystyle x = [a_0,a_1, \ldots, a_{n-1},\frac{1}{t_{n-1}}]
=[a_0,a_1, \ldots, a_{n-1},a_n + t_n]
=[a_0,a_1, \ldots, a_{n-1},a_n, \frac{1}{t_n}].$](img38.png)
![]()
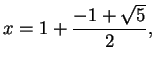
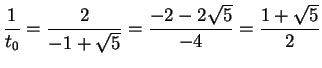
? contfrac(exp(1))
%1 = [2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1,
12, 1, 1, 14, 1, 1, 16, 1, 1, 18, 1, 1, 20, 2]
? \\ to get more terms, increase the real precision:
? \p60
? contfrac(exp(1),[])
%12 = [2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1,
12, 1, 1, 14, 1, 1, 16, 1, 1, 18, 1, 1, 20, 1, 1, 22, 1,
1, 24, 1, 1, 26, 1, 1, 28, 1, 1, 30, 1, 1, 32, 1, 1, 34,
1, 1, 36, 1, 1, 38, 1, 1, 40, 1, 1, 42, 2]
The following program uses a proposition we proved yesterday to compute the partial convergents
of a continued fraction:
{convergents(v)=
local(pp,qq,p,q,tp,tq,answer);
pp=1; qq=0; p=v[1]; q=1; \\ pp is p_{n-1} and p is p_n.
answer = vector(length(v)); \\ put answer in this vector
answer[1] = p/q;
for(n=2,length(v),
tp=p; tq=q; p=v[n]*p+pp; q=v[n]*q+qq; pp=tp; qq=tq;
answer[n] = p/q;
);
return(answer);
}
Let's try this with ![]() :
:
? contfrac(Pi) %26 = [3, 7, 15, 1, 292, 1, 1, ...] ? convergents([3,7,15]) %27 = [3, 22/7, 333/106] ? convergents([3,7,15,1,292]) %28 = [3, 22/7, 333/106, 355/113, 103993/33102] ? %[5]*1.0 %29 = 3.1415926530119026040... ? % - Pi %30 = -0.000000000577890634...