Proof.
First suppose that
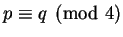
. By swapping
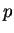
and
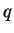
if
necessary, we may assume that
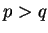
, and write
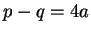
.
Since
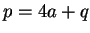
,
and
Proposition
2.2 implies that
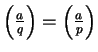
, since
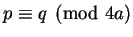
. Thus
where the last equality is because
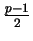
is even
if and only if
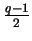
is even.
Next suppose that
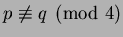 , so
, so
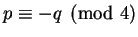 .
Write
.
Write 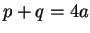 . We have
. We have
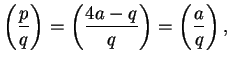
and
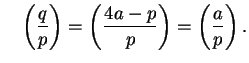
Since
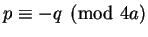
, Proposition
2.2
implies that
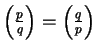
.
Since
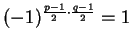
, the
proof is complete.

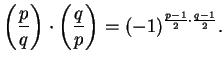
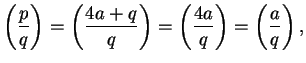
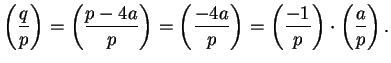
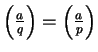 , since
, since
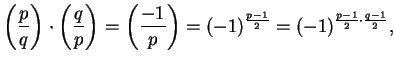
![]() , so
, so
![]() .
Write
.
Write ![]() . We have
. We have
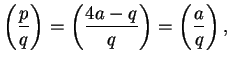 and
and 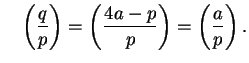
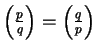 .
Since
.
Since