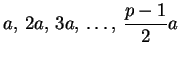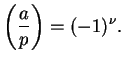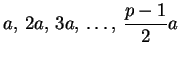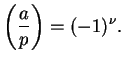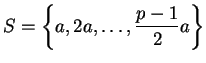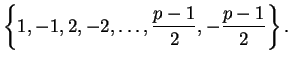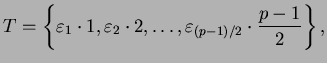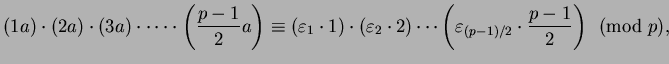A Lemma of Gauss

The proof we will give of Theorem 2.1 was first discovered by Gauss, though not when he was $19$. This proof is given in many elementary number theory texts (including Davenport). It depends on the following lemma of Gauss:

Lemma 3.1   Let $p$ be an odd prime and let $a$ be an integer $\not\equiv 0\pmod{p}$. Form the numbers

$$a,\, 2a,\, 3a,\, \ldots,\, \frac{p-1}{2} a$$

and reduce them modulo $p$ to lie in the interval $(-\frac{p}{2},\,\, \frac{p}{2})$. Let $\nu$ be the number of negative numbers in the resulting set. Then

$$\left(\frac{a}{p}\right) = (-1)^{\nu}.$$

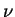
Proof. In defining $\nu$, we expressed each number in

$$S = \left\{a, 2a, \ldots, \frac{p-1}{2} a\right\}$$

as congruent to a number in the set

$$\left\{ 1, -1, 2, -2, \ldots, \frac{p-1}{2}, -\frac{p-1}{2}\right\}.$$

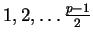
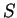
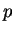
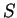
No number $1, 2, \ldots \frac{p-1}{2}$ appears more than once, with either choice of sign, because if it did then either two elements of $S$ are congruent modulo $p$ or 0 is the sum of two elements of $S$, and both events are impossible. Thus the resulting set must be of the form

$$T = \left\{\varepsilon _1\cdot 1, \varepsilon _2 \cdot 2, \ldots, \varepsilon _{(p-1)/2}\cdot \frac{p-1}{2} \right\},$$

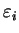
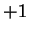
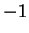
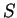
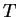
where each $\varepsilon _i$ is either $+1$ or $-1$. Multiplying together the elements of $S$ and of $T$, we see that

$$(1a) \cdot (2a)\cdot(3a)\cdot \cdots \cdot \left(\frac{p-1}{2} a\... ...ot 2) \cdots \left(\varepsilon _{(p-1)/2} \cdot \frac{p-1}{2}\right)\pmod{p},$$

so

$$a^{(p-1)/2} \equiv \varepsilon _1\cdot \varepsilon _2\cdot \cdots \cdot \varepsilon _{(p-1)/2}\pmod{p}.$$

The lemma then follows from Proposition 1.1. $\qedsymbol$