2i. On input
Math 124 Problem Set 6
1. -389 is negative, and thus not the sum of two squares.
Since ![]() , it is not the sum of two squares. Since
, it is not the sum of two squares. Since
![]() , it is not the sum of two squares.
, it is not the sum of two squares. ![]() is a
perfect square. Since
is a
perfect square. Since ![]() , it is not the sum of two
squares. Finally,
, it is not the sum of two
squares. Finally,
![]() and
and
![]() , so it
is not the sum of two squares.
, so it
is not the sum of two squares.
2i. On input ![]() , the program breaks up
, the program breaks up ![]() into two
parts and looks for a sum of two squares representation.
into two
parts and looks for a sum of two squares representation.
{squares(n) = local(y); for(x=1,floor(sqrt(n)),
y=sqrt(n-![]() );
);
if(y-floor(y)==0, return([x,floor(y)]))
);
return(0) }
f(n) =
for(x=1,n,
a=squares(x);
b=squares(n-x);
if(a!=0 && b!=0, return([a,b])));}
2ii.
![]() .
.
3. 625 There are two Pythagorean triples with
25 as the hypotenuse: ![]() and
and
![]() . This gives
two representations of 625 as the sum of two squares. Of course,
. This gives
two representations of 625 as the sum of two squares. Of course,
![]() is a third.
is a third.
4. The forward direction is trivial. For the opposite
direction, suppose that ![]() is the sum of two rational squares:
is the sum of two rational squares:
![]() , but it is not the sum of two
integer squares. Then
, but it is not the sum of two
integer squares. Then ![]() , where
, where
![]() is a
prime factor and
is a
prime factor and ![]() is odd. Now,
is odd. Now,
![]() , so
, so
![]() is the sum of two integer squares. However, all the
prime factors of
is the sum of two integer squares. However, all the
prime factors of ![]() have even exponent, so
have even exponent, so
![]() ,
where
,
where ![]() is still odd. This is a contradiction; therefore
is still odd. This is a contradiction; therefore ![]() must be the sum of two integer squares.
must be the sum of two integer squares.
5. Suppose
![]() , where
, where ![]() is an odd prime and
is an odd prime and
![]() are integers. Then
are integers. Then
![]() , so
, so
![]() (since
(since ![]() is a field). From
Lecture 13,
is a field). From
Lecture 13,
![]() iff
iff
![]() . Also,
. Also,
![]() iff
iff
![]() . Since
. Since
![]() , we have
, we have
![]() iff
iff
![]() .
.
Conversely, suppose
![]() is
prime. Let
is
prime. Let ![]() be such that
be such that
![]() . Taking
. Taking
![]() and applying Lemma 1.3 from Lecture
21, there exist integers
and applying Lemma 1.3 from Lecture
21, there exist integers ![]() with
with
![]() such that
such that
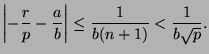
9. The discriminants are equal:
![]() . However, the forms are not
equivalent. To see this, we first show that
. However, the forms are not
equivalent. To see this, we first show that
![]() is equivalent to
is equivalent to ![]() . As above, this means solving
. As above, this means solving