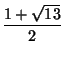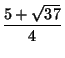Next: About this document ...
Homework 5: Continued Fractions
DUE WEDNESDAY, OCTOBER 31 (HALLOWEEN)
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
There are 10 problems. Feel free to use a computer on any of
them.
- 1.
- (3 points) Draw some
sort of diagram that illustrates the partial convergents
of the following continued fractions:
- (i)
-
![$ [13,1,8,3]$](img2.png)
- (ii)
-
![$ [1,1,1,1,1,1,1,1]$](img3.png)
- (iii)
-
![$ [1,2,3,4,5,6,7,8]$](img4.png)
- 2.
- (5 points)
If
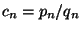 is the
is the 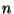 th convergent of the continued fraction
th convergent of the continued fraction
![$ [a_0,a_1,\ldots,a_n]$](img7.png) and
and 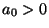 , show that
and
(Hint: In the first case, notice that
, show that
and
(Hint: In the first case, notice that
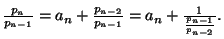 )
)
- 3.
- (4 points) There is a function
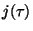 , denoted by ellj in PARI, which takes as input a complex number
, denoted by ellj in PARI, which takes as input a complex number  with
positive imaginary part, and returns a complex number called the
``
with
positive imaginary part, and returns a complex number called the
``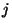 -invariant of the associated elliptic curve''. Suppose
that
-invariant of the associated elliptic curve''. Suppose
that 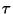 is approximately
is approximately
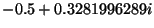 and that you
know that
and that you
know that 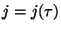 is a rational number. Use continued fractions
and PARI to compute a reasonable guess for the rational number
is a rational number. Use continued fractions
and PARI to compute a reasonable guess for the rational number
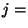 ellj
ellj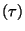 . (Hint: In PARI
. (Hint: In PARI 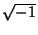 is represented
by I.)
is represented
by I.)
- 4.
- (3 points) Evaluate each of the following infinite continued fractions:
- (iv)
-
![$ [\overline{2,3}]$](img20.png)
- (v)
-
![$ [2,\overline{1,2,1}]$](img21.png)
- (vi)
-
![$ [0,\overline{1,2,3}]$](img22.png)
- 5.
- (3 points) Determine the infinite continued fraction of each of the following
numbers:
- (vii)
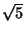
- (viii)
-
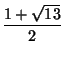
- (ix)
-
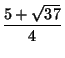
- 6.
- (x)
- (4 points) For any positive integer
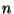 , prove that
, prove that
![$ \sqrt{n^2+1} = [n,\overline{2n}].$](img26.png)
- (xi)
- (2 points)
Find a convergent to
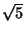 that approximates
that approximates 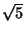 to within four decimal places.
to within four decimal places.
- 7.
- (4 points) A famous theorem of
Hurwitz (1891) says that for any irrational
number
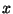 , there exists infinitely many rational numbers
, there exists infinitely many rational numbers 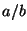 such that
Taking
such that
Taking 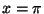 , obtain three rational numbers that satisfy this
inequality.
, obtain three rational numbers that satisfy this
inequality.
- 8.
- (3 points) The continued fraction expansion of
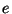 is
It is a theorem that the obvious pattern continues indefinitely. Do
you think that the continued fraction expansion of
is
It is a theorem that the obvious pattern continues indefinitely. Do
you think that the continued fraction expansion of 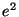 also exhibits
a nice pattern? If so, what do you think it is?
also exhibits
a nice pattern? If so, what do you think it is?
- 9.
- (xii)
- (4 points) Show that there are infinitely many even integers
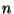 with the property that both
with the property that both 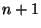 and
and
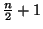 are perfect
squares.
are perfect
squares.
- (xiii)
- (3 points) Exhibit two such integers that are greater than
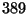 .
.
- 10.
- (7 points)
A primitive Pythagorean triple is a triple
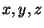 of integers
such that
of integers
such that
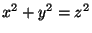 .
Prove that there exists infinitely many primitive Pythagorean
triples
.
Prove that there exists infinitely many primitive Pythagorean
triples 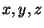 in which
in which 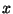 and
and 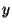 are consecutive integers.
are consecutive integers.



Next: About this document ...
William A Stein
2001-10-28
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001