


Next: About this document ...
Homework 3: Public-Key Cryptography
DUE WEDNESDAY, OCTOBER 10
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
Cite sources of help, work with other students,
and come see me during office hours (WF at 2pm). Feel free
to make unrestricted use of PARI in problems 1-7.
- (3 points) You and Nikita wish to agree on a secret key using
the Diffie-Hellman protocol. Nikita announces that
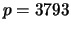 and
and
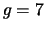 . Nikita secretely chooses a number
. Nikita secretely chooses a number 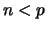 and tells you
that
and tells you
that
 . You choose the random number
. You choose the random number
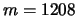 . Tell me what the secret key is!
. Tell me what the secret key is!
- (4 points) This problem concerns encoding phrases using numbers.
- Find the number that corresponds to
VE RI TAS, where we view this string as a number in
base 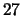 using the encoding of Section 2 of Lecture 9.
(Note that the left-most ``digit'',
using the encoding of Section 2 of Lecture 9.
(Note that the left-most ``digit'', V, is the
least significant digit, and denotes a blank space.)
- What is the longest sequence of letters (and space) that
can be stored using a number that is less than
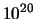 ?
?
- (4 points) You see Michael and
Nikita agree on a secret key using the Diffie-Hellman key exchange
protocol. Michael and Nikita choose
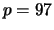 and
and 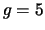 . Nikita chooses
a random number
. Nikita chooses
a random number 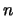 and tells Michael that
and tells Michael that
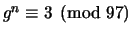 , and
Michael chooses a random number
, and
Michael chooses a random number 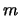 and tells Nikita that
and tells Nikita that
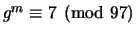 . Crack their code: What is the secret key that Nikita and
Michael agree upon? What is
. Crack their code: What is the secret key that Nikita and
Michael agree upon? What is 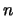 ? What is
? What is 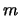 ?
?
- (2 points)
Using the RSA public key is
 ,
encrypt the year that you will graduate from Harvard.
,
encrypt the year that you will graduate from Harvard.
- (6 points) In this problem, you will ``crack'' an RSA cryptosystem.
- What is the secret decoding number
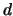 for the RSA
cryptosystem with public key
for the RSA
cryptosystem with public key
 ?
?
- The number
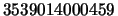 encrypts an important question using
the RSA cryptosystem from part (a). What is the question? (After decoding,
you'll get a number. To find the corresponding word, see Section 2 of
Lecture 9.)
encrypts an important question using
the RSA cryptosystem from part (a). What is the question? (After decoding,
you'll get a number. To find the corresponding word, see Section 2 of
Lecture 9.)
- (4 points)
Suppose Michael creates an RSA cryptosystem with a very large
modulus
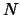 for which the factorization of
for which the factorization of 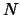 cannot be found
in a reasonable amount of time. Suppose that Nikita sends
messages to Michael by representing each alphabetic character
as an integer between 0 and
cannot be found
in a reasonable amount of time. Suppose that Nikita sends
messages to Michael by representing each alphabetic character
as an integer between 0 and 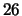 (
(A corresponds
to 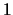 ,
, B to 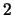 , etc., and a space
, etc., and a space to 0),
then encrypts each number separately
using Michael's RSA cryptosystem. Is this method secure?
Explain your answer.
- (6 points)
Nikita creates an RSA cryptosystem with public key
In the following two problems, show the steps you take.
Don't simply factor
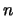 directly using the factor
function in PARI.
directly using the factor
function in PARI.
- Somehow you discover that
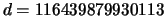 . Show how to use the
probabilistic algorithm of Lecture 10 to use
. Show how to use the
probabilistic algorithm of Lecture 10 to use 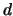 to factor
to factor 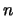 .
.
- In part (a) you found that the factors
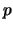 and
and 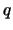 of
of 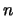 are very close.
Show how to use
the ``Fermat Factorization'' method of Lecture 10 to factor
are very close.
Show how to use
the ``Fermat Factorization'' method of Lecture 10 to factor 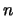 .
.



Next: About this document ...
William A Stein
2001-10-05
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001