



Next: A way to compute
Up: The Naive Algorithms
Previous: The Naive Algorithms
Contents
Use the (not-exact!) sequence:
The composition map from
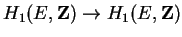 is multiplication by
is multiplication by 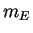 , and
, and
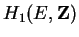 can be
computed because its image in
can be
computed because its image in
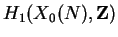 is
saturated, as
is
saturated, as 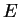 is optimal.
This algorithm is described in detail in [Kohel-Stein, ANTS IV],
and amounts to finding ``left and right eigenvectors'' and taking
their dot product.
is optimal.
This algorithm is described in detail in [Kohel-Stein, ANTS IV],
and amounts to finding ``left and right eigenvectors'' and taking
their dot product.
William A Stein
2002-09-29