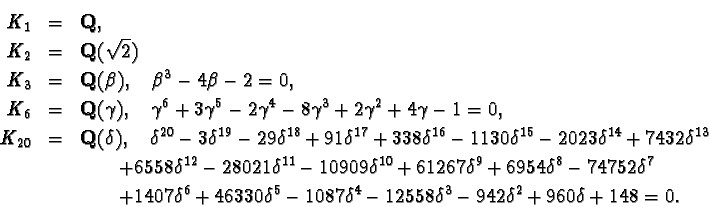Next: PARI code
Up: The unusual Hecke algebra X(389)
Previous: Basis of eigenforms
The discriminant of the
Hecke algebra
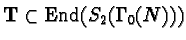 is the discriminant
with respect to the trace pairing. The ring
is the discriminant
with respect to the trace pairing. The ring
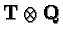 is a product
is a product
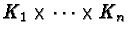 of totally real number fields.
Let
of totally real number fields.
Let
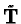 denote the integral closure of
T in
denote the integral closure of
T in
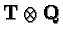 ;
note that
;
note that
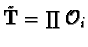 where
where 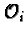 is the ring
of integers of Ki.
The discriminant of
T also equals
is the ring
of integers of Ki.
The discriminant of
T also equals
![$[\tilde{\mathbf{T}}:\mathbf{T}]\cdot \prod_{i=1}^n\mbox{\rm disc}(K_i)$](img23.gif) .
.
We view the
primes dividing
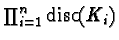 as arising from
singularities of the individual irreducible
components of
as arising from
singularities of the individual irreducible
components of
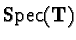 .
The primes dividing
.
The primes dividing
![$[\tilde{\mathbf{T}}:\mathbf{T}]$](img26.gif) are viewed as arising from intersections of irreducible
components, or what is the same, congruences between eigenforms.
are viewed as arising from intersections of irreducible
components, or what is the same, congruences between eigenforms.
The discriminant of the Hecke algebra
T associated to
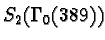 is
is
This discriminant was computed by applying the definition of
discriminant to a representation of the first 65 Hecke
operators
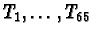 .
Matrices representing these
Hecke operators were computed using the modular symbols algorithms
described in [Cremona, Algorithms for modular elliptic curves].
The number 65=390/6 of Hecke operators needed to generate
Tas a
Z-module was chosen in accord with the bound in
[Sturm, On the congruence of modular forms].
.
Matrices representing these
Hecke operators were computed using the modular symbols algorithms
described in [Cremona, Algorithms for modular elliptic curves].
The number 65=390/6 of Hecke operators needed to generate
Tas a
Z-module was chosen in accord with the bound in
[Sturm, On the congruence of modular forms].
In the case of X0(389),
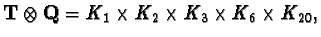 where Kd has degree d over
Q.
We have
where Kd has degree d over
Q.
We have
The discriminants of the Ki are
Observe that the discriminant of K20 is divisible by 389;
this is the unusual behavior alluded to in the introduction.
The product of the discriminants is
This differs from the exact discriminant by a factor
of
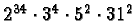 ,
so
the index of
T in its normalization is
,
so
the index of
T in its normalization is
Notice that 389 does not divide this index, and that 389 is not
a ``congruence prime''; thus 389 does not divide any
modular degrees. We do not know of any examples of
optimal quotients of J0(p) such that p divides the modular
degree.



Next: PARI code
Up: The unusual Hecke algebra X(389)
Previous: Basis of eigenforms
William A. Stein
1999-10-21
![]() as arising from
singularities of the individual irreducible
components of
as arising from
singularities of the individual irreducible
components of
![]() .
The primes dividing
.
The primes dividing
![]() are viewed as arising from intersections of irreducible
components, or what is the same, congruences between eigenforms.
are viewed as arising from intersections of irreducible
components, or what is the same, congruences between eigenforms.
![]() is
is
![]() where Kd has degree d over
Q.
We have
where Kd has degree d over
Q.
We have