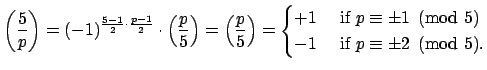Suppose
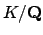 is a quadratic field. Then
is a quadratic field. Then 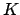 is Galois, so for each prime
is Galois, so for each prime
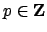 we have
we have
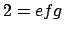 . There are exactly three possibilties:
. There are exactly three possibilties:
- Ramified:
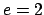 ,
, 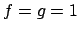 : The prime
: The prime 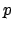 ramifies in
ramifies in 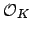 , so
, so
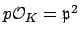 .
There are only finitely many such primes, since if
.
There are only finitely many such primes, since if 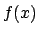 is the minimal polynomial
of a generator for
is the minimal polynomial
of a generator for 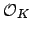 , then
, then 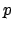 ramifies if and only if
ramifies if and only if 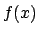 has a multiple root
modulo
has a multiple root
modulo 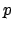 . However,
. However, 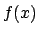 has a multiple root modulo
has a multiple root modulo 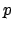 if and only if
if and only if 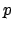 divides
the discriminant of
divides
the discriminant of 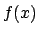 , which is nonzero because
, which is nonzero because 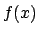 is irreducible over
is irreducible over
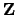 .
(This argument shows there are only finitely many ramified primes in any number field.
In fact, we will later show that the ramified primes are exactly the ones that
divide the discriminant.)
.
(This argument shows there are only finitely many ramified primes in any number field.
In fact, we will later show that the ramified primes are exactly the ones that
divide the discriminant.)
- Inert:
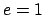 ,
, 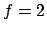 ,
, 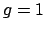 : The prime
: The prime 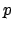 is inert in
is inert in 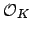 , so
, so
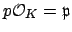 is prime. This happens 50% of the time, which is
suggested by quadratic reciprocity (but not proved this way),
as we will see illustrated below for a particular example.
is prime. This happens 50% of the time, which is
suggested by quadratic reciprocity (but not proved this way),
as we will see illustrated below for a particular example.
- Split:
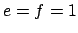 ,
, 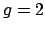 : The prime
: The prime 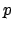 splits in
splits in 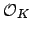 , in the
sense that
, in the
sense that
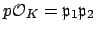 with
with
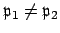 . This happens the other
50% of the time.
. This happens the other
50% of the time.
Suppose, in particular, that
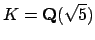 , so
, so
![$ \O _K=\mathbf{Z}[\gamma]$](img913.png) ,
where
,
where
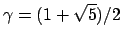 . Then
. Then 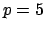 is ramified, since
is ramified, since
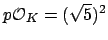 .
More generally, the order
.
More generally, the order
![$ \mathbf{Z}[\sqrt{5}]$](img356.png) has index
has index 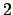 in
in 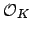 , so for any prime
, so for any prime 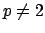 we can
determine the factorization of
we can
determine the factorization of 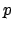 in
in 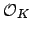 by finding the factorization of the
polynomial
by finding the factorization of the
polynomial
![$ x^2-5\in \mathbf{F}_p[x]$](img1224.png) . The polynomial
. The polynomial 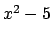 splits as a product of two
distinct factors in
splits as a product of two
distinct factors in
![$ \mathbf{F}_p[x]$](img220.png) if and only if
if and only if 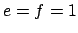 and
and 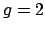 . For
. For 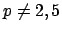 this is the
case if and only if
this is the
case if and only if 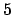 is a square in
is a square in
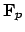 , i.e., if
, i.e., if
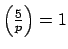 , where
, where
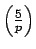 is
is 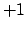 if
if 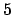 is a square mod
is a square mod 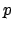 and
and 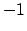 if
if 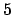 is not.
By quadratic reciprocity,
Thus whether
is not.
By quadratic reciprocity,
Thus whether 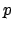 splits or is inert in
splits or is inert in 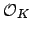 is determined by the residue class of
is determined by the residue class of 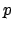 modulo
modulo 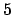 .
.
William Stein
2004-05-06