Kolyvagin's Euler System: Compute it
Immediate Tasks
Implement the Silverman height bound from here: http://www.jstor.org/stable/2008444?seq=3 This works over all fields at once, and is easy to code up, and should be fine for our application.
Describing Dokchitser parameters for
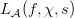 , where
, where 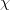 is any character of
is any character of 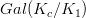 . This will involve efficient computation of theta series, characters, etc.
. This will involve efficient computation of theta series, characters, etc. Use Dokchitser to provably compute some number of digits of the height of
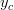 , so that later we can compute all points with that height.
, so that later we can compute all points with that height. Figure out how to saturate Mordell-Weil group of
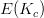 by reducing modulo many primes and doing a small point search. (Look up, read, and precisely write down how we know this curve has rank 1. This is Bertolini-Darmon: (1) we compute
by reducing modulo many primes and doing a small point search. (Look up, read, and precisely write down how we know this curve has rank 1. This is Bertolini-Darmon: (1) we compute 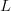 and find that order of vanishing is 1, so get structure theorem for Selmer just like over
and find that order of vanishing is 1, so get structure theorem for Selmer just like over 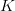 .
. Once we have computed generators for
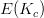 , we enumerate all points of height the height of the Heegner point
, we enumerate all points of height the height of the Heegner point 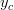 , according to Dokchitser. We can do this by enumerating lattice points, which is standard. We then recognize which point is
, according to Dokchitser. We can do this by enumerating lattice points, which is standard. We then recognize which point is 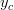 because there will be exactly one whose floating point approximation is closest to the points we just computed with the right height. Thus we are replacing having infinitely many possibilities for our floating point approximation to
because there will be exactly one whose floating point approximation is closest to the points we just computed with the right height. Thus we are replacing having infinitely many possibilities for our floating point approximation to 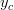 by having only finitely many.
by having only finitely many.
