We can compute the Galois group of the Galois closure as an abstract “Pari group” using the galois_group function, which by default calls Pari (http://pari.math.u-bordeaux.fr/). You do not have to worry about installing Pari, since Pari is part of Sage. In fact, despite appearances much of the difficult algebraic number theory in Sage is actually done by the Pari C library (be sure to also cite Pari in papers that use Sage).
sage: K.<alpha> = NumberField(x^3 - 2)
sage: G = K.galois_group()
sage: G
Galois group PARI group [6, -1, 2, "S3"] of degree 3 of the
Number Field in alpha with defining polynomial x^3 - 2
We can find out more about 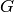 , too:
, too:
sage: G.order()
6
We compute two more Galois groups of degree 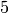 extensions, and
see that one has Galois group
extensions, and
see that one has Galois group 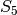 , so is not solvable by
radicals:
, so is not solvable by
radicals:
sage: NumberField(x^5 - 2, 'a').galois_group()
Galois group PARI group [20, -1, 3, "F(5) = 5:4"] of
degree 5 of the Number Field in a with defining
polynomial x^5 - 2
sage: NumberField(x^5 - x + 2, 'a').galois_group()
Galois group PARI group [120, -1, 5, "S5"] of degree 5 of
the Number Field in a with defining polynomial x^5 - x + 2
Recent versions of Magma have an algorithm for computing Galois groups that in theory applies when the input polynomial has any degree. There are no open source implementation of this algorithm (as far as I know). If you have Magma, you can use this algorithm from Sage by calling the galois_group function and giving the algorithm='magma' option.
sage: K.<a> = NumberField(x^3 - 2)
sage: K.galois_group(algorithm='magma') # optional
verbose...
Galois group Transitive group number 2 of degree 3 of
the Number Field in a with defining polynomial x^3 - 2
We emphasize that the above example should not work if you don’t have Magma.
It is also possible to work explicitly with the group of automorphisms of a field (though the link in Sage between abstract groups and automorphisms of fields is currently poor.
Note
An excellent Sage development project would be to make it so Sage supports finding the abstract group structure of automorphism groups of fields; i.e., make the automorphism group more than just a set.
For example, here we first define ![\mathbb{Q}(\sqrt[3]{2})](_images/math/5852935b5a3b8a599dc13f1b75b5de8f7bff5484.png) ,
then compute its Galois closure, which we represent as
,
then compute its Galois closure, which we represent as
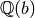 , where
, where 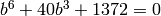 . Then we
compute the automorphism group of the field
. Then we
compute the automorphism group of the field 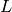 , and explicitly
list its elements.
, and explicitly
list its elements.
sage: K.<a> = NumberField(x^3 - 2)
sage: L.<b> = K.galois_closure()
sage: L
Number Field in b with defining polynomial x^6 + 40*x^3 + 1372
sage: G = Hom(L, L)
sage: G
Automorphism group of Number Field in b ...
sage: G.list()
[
Ring endomorphism of Number Field in b ...
Defn: b |--> b,
Ring endomorphism of Number Field in b ...
Defn: b |--> 1/36*b^4 + 1/18*b,
...
Ring endomorphism of Number Field in b ...
Defn: b |--> -2/63*b^4 - 31/63*b
]
You can explicitly apply any of the automorphisms above to any
elements of 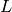 .
.
sage: phi = G.list()[1]
sage: phi
Ring endomorphism of Number Field in b ...
Defn: b |--> 1/36*b^4 + 1/18*b
sage: phi(b^2 + 2/3*b)
-1/36*b^5 + 1/54*b^4 - 19/18*b^2 + 1/27*b
You can also enumerate all complex embeddings of a number field:
sage: K.complex_embeddings()
[
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Complex Double Field
Defn: a |--> -0.629960524947 - 1.09112363597*I,
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Complex Double Field
Defn: a |--> -0.629960524947 + 1.09112363597*I,
Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Complex Double Field
Defn: a |--> 1.25992104989
]
The class group 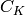 of a number field
of a number field 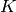 is the group
of fractional ideals of the maximal order
is the group
of fractional ideals of the maximal order 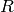 of
of 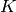 modulo the subgroup of principal fractional ideals. One of the main
theorems of algebraic number theory asserts that
modulo the subgroup of principal fractional ideals. One of the main
theorems of algebraic number theory asserts that 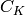 is a
finite group. For example, the quadratic number field
is a
finite group. For example, the quadratic number field
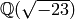 has class number
has class number 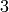 , as we see
using the Sage class number command.
, as we see
using the Sage class number command.
sage: L.<a> = NumberField(x^2 + 23)
sage: L.class_number()
3
There are only 9 quadratic imaginary field
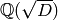 that have class number
that have class number 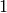 :
:
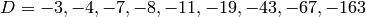
To find this list using Sage, we first experiment with making lists
in Sage. For example, typing [1..10] makes the
list of integers between 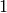 and
and 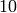 .
.
sage: [1..10]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
We can also make the list of odd integers between 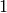 and
and
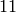 , by typing [1,3,..,11], i.e., by giving the second term
in the arithmetic progression.
, by typing [1,3,..,11], i.e., by giving the second term
in the arithmetic progression.
sage: [1,3,..,11]
[1, 3, 5, 7, 9, 11]
Applying this idea, we make the list of negative numbers from
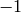 down to
down to 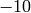 .
.
sage: [-1,-2,..,-10]
[-1, -2, -3, -4, -5, -6, -7, -8, -9, -10]
The first two lines below makes a list  of every
of every 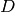 from
from 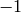 down to
down to 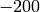 such that
such that 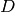 is a
fundamental discriminant (the discriminant of a quadratic imaginary
field).
is a
fundamental discriminant (the discriminant of a quadratic imaginary
field).
Note
Note that you will not see the ... in the output below; this ... notation just means that part of the output is omitted below.
sage: w = [-1,-2,..,-200]
sage: v = [D for D in w if is_fundamental_discriminant(D)]
sage: v
[-3, -4, -7, -8, -11, -15, -19, -20, ..., -195, -199]
Finally, we make the list of 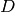 in our list
in our list  such that
the quadratic number field
such that
the quadratic number field 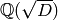 has class
number
has class
number 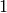 . Notice that QuadraticField(D) is a shorthand for
NumberField(x^2 - D).
. Notice that QuadraticField(D) is a shorthand for
NumberField(x^2 - D).
sage: [D for D in v if QuadraticField(D,'a').class_number()==1]
[-3, -4, -7, -8, -11, -19, -43, -67, -163]
Of course, we have not proved that this is the list of all
negative  so that
so that 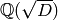 has
class number
has
class number 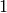 .
.
A frustrating open problem is to prove that there are infinitely many
number fields with class number 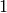 . It is quite easy to be
convinced that this is probably true by computing a bunch of class
numbers of real quadratic fields. For example, over 58 percent of the
real quadratic number fields with discriminant
. It is quite easy to be
convinced that this is probably true by computing a bunch of class
numbers of real quadratic fields. For example, over 58 percent of the
real quadratic number fields with discriminant 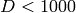 have
class number
have
class number 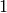 !
!
sage: w = [1..1000]
sage: v = [D for D in w if is_fundamental_discriminant(D)]
sage: len(v)
302
sage: len([D for D in v if QuadraticField(D,'a').class_number() == 1])
176
sage: 176.0/302
0.582781456953642
For more intuition about what is going on, read about the Cohen-Lenstra heuristics.
Sage can also compute class numbers of extensions of higher degree,
within reason. Here we use the shorthand CyclotomicField(n) to
create the number field 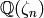 .
.
sage: CyclotomicField(7)
Cyclotomic Field of order 7 and degree 6
sage: for n in [2..15]: print n, CyclotomicField(n).class_number()
2 1
3 1
...
15 1
In the code above, the notation for n in [2..15]: ... means
“do ... for 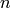 equal to each of the integers
equal to each of the integers 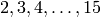 .”
.”
Note
Exercise: Compute what is omitted (replaced by ...) in the output of the previous example.
Computations of class numbers and class groups in Sage is done by the
Pari C library, and unlike in Pari, by default Sage tells Pari not
to assume any conjectures. This can make some commands vastly slower
than they might be directly in Pari, which does assume unproved
conjectures by default. Fortunately, it is easy to tell Sage to be
more permissive and allow Pari to assume conjectures, either just for
this one call or henceforth for all number field functions. For
example, with proof=False it takes only a few seconds to verify,
modulo the conjectures assumed by Pari, that the class number of
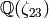 is
is 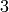 .
.
sage: CyclotomicField(23).class_number(proof=False)
3
Note
Exercise: What is the smallest 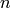 such that
such that
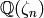 has class number bigger than
has class number bigger than 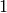 ?
?
In addition to computing class numbers, Sage can also compute the
group structure and generators for class groups. For example, the
quadratic field 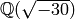 has class group
has class group
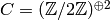 , with generators the
ideal classes containing
, with generators the
ideal classes containing 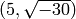 and
and
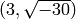 .
.
sage: K.<a> = QuadraticField(-30)
sage: C = K.class_group()
sage: C
Class group of order 4 with structure C2 x C2 of Number Field
in a with defining polynomial x^2 + 30
sage: category(C)
Category of groups
sage: C.gens()
[Fractional ideal class (5, a), Fractional ideal class (3, a)]
In Sage, the notation C.i means “the 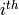 generator of the
object
generator of the
object 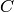 ,” where the generators are indexed by numbers
,” where the generators are indexed by numbers
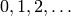 . Below, when we write C.0 \* C.1, this
means “the product of the 0th and 1st generators of the class group
. Below, when we write C.0 \* C.1, this
means “the product of the 0th and 1st generators of the class group
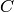 .”
.”
sage: K.<a> = QuadraticField(-30)
sage: C = K.class_group()
sage: C.0
Fractional ideal class (5, a)
sage: C.0.ideal()
Fractional ideal (5, a)
sage: I = C.0 * C.1
sage: I
Fractional ideal class (2, a)
Next we find that the class of the fractional ideal
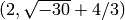 is equal to the ideal class
is equal to the ideal class
 .
.
sage: A = K.ideal([2, a+4/3])
sage: J = C(A)
sage: J
Fractional ideal class (2/3, 1/3*a)
sage: J == I
True
Unfortunately, there is currently no Sage function that writes a fractional ideal class in terms of the generators for the class group.