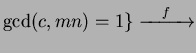 |
||
The map ![]() is injective: If
is injective: If
![]() , then
, then
![]() and
and
![]() , so, since
, so, since
![]() ,
,
![]() , so
, so ![]() .
.
The map ![]() is surjective: Given
is surjective: Given ![]() with
with
![]() ,
,
![]() , the Chinese Remainder Theorem implies that there
exists
, the Chinese Remainder Theorem implies that there
exists ![]() with
with
![]() and
and
![]() . We
may assume that
. We
may assume that
![]() , ans since
, ans since
![]() and
and
![]() , we must have
, we must have
![]() . Thus
. Thus
![]() .
.
Because ![]() is a bijection, the set on the left has the same
size as the product set on the right. Thus
is a bijection, the set on the left has the same
size as the product set on the right. Thus
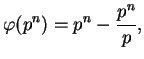
? eulerphi(389*11^2) %15 = 42680