Next: Continued Fractions of Algebraic Up: Quadratic Irrationals Previous: Quadratic Irrationals Contents Index
for some fixed positive integer
![$\displaystyle [\overline{1,2}] = 1+\frac{1}{\displaystyle 2+\frac{1}{\displaystyle 1+\frac{1}{\displaystyle 2+ \frac{1}{\displaystyle 1+\cdots}}}},$](img1882.png)
so if
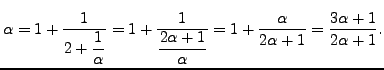
Thus
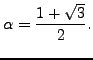
is a periodic continued fraction. Set
so by Proposition 5.1.5
Here we use that
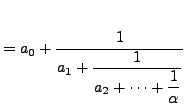 |
The continued fraction procedure
applied to the value of an infinite simple continued fraction
yields that continued fraction back, so
by Proposition 5.2.12,
![]() because it is the
value of an infinite continued fraction.
because it is the
value of an infinite continued fraction.
(
![]() )
Suppose
)
Suppose
![]() is an irrational number that satisfies a quadratic equation
is an irrational number that satisfies a quadratic equation
so
We will prove periodicity by showing that the set of
It remains to show there are only finitely many distinct ![]() . We
have
. We
have
Substituting this expression for
where
Recall from the proof of Theorem 5.2.10 that
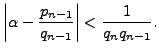
Thus
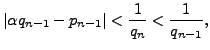
so
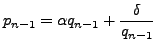 with
with Hence
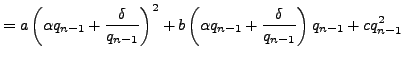 |
||
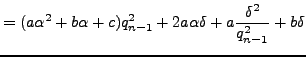 |
||
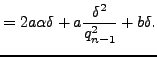 |
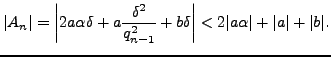
Thus there are only finitely many possibilities for the integer
so there are only finitely many triples
William 2007-06-01