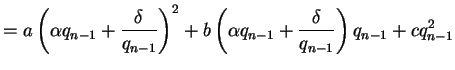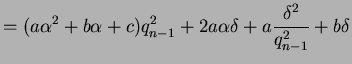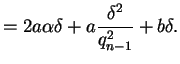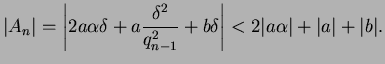Definition 2.1
A
periodic continued fraction is a continued
fraction
![$ [a_0, a_1, \ldots, a_n, \ldots]$](img10.png)
such that
for a fixed positive integer
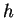
and all sufficiently large
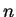
.
We call
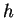
the
period of the continued fraction.
Proof.
(

) First suppose that
is a periodic continued fraction. Set
![$ \alpha=[a_{n+1},a_{n+2}, \ldots]$](img24.png)
. Then
so
(We use that
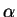
is the last partial convergent.)
Thus
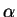
satisfies a quadratic equation. Since the
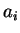
are
all integers, the number
can be expressed as a polynomial in
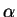
with
rational coefficients, so
![$ [a_0, a_1, \ldots]$](img32.png)
also satisfies a quadratic polynomial.
Finally,
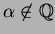
because periodic continued fractions
have infinitely many terms.
(
 )
This direction was first proved by Lagrange. The proof
is much more exciting!
Suppose
)
This direction was first proved by Lagrange. The proof
is much more exciting!
Suppose
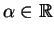 satisfies a quadratic equation
satisfies a quadratic equation
with
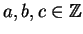
.
Let
![$ [a_0, a_1, \ldots]$](img32.png)
be the expansion of
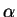
. For each
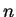
, let
so that
We have
Substituting this expression for
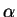
into the quadratic equation
for
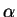
, we see that
where
Note that
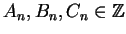
, that
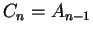
, and that
Recall from the proof of Theorem 2.3 of the previous lecture that
Thus
so
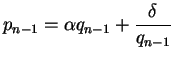
with
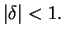
Hence
Thus
Thus there are only finitely many possibilities for the integer
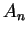
.
Also,
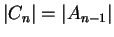
and
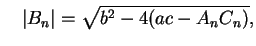
so there are only finitely many triples
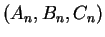
,
and hence only finitely many possibilities for
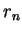
as
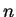
varies. Thus for some
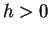
,
This shows that the continued fraction for
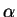
is periodic.

![$\displaystyle [\overline{1,2}] = 1+\frac{1}{2+\frac{1}{1+\frac{1}{2+ \frac{1}{1+\cdots}}}},$](img15.png)
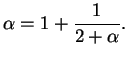
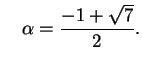
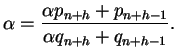
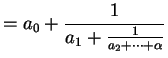
![]() )
This direction was first proved by Lagrange. The proof
is much more exciting!
Suppose
)
This direction was first proved by Lagrange. The proof
is much more exciting!
Suppose
![]() satisfies a quadratic equation
satisfies a quadratic equation
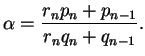
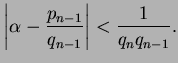
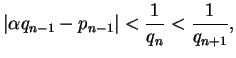
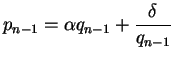 with
with