Computing with Newforms¶
In this chapter we pull together results and algorithms from Chapter Modular Forms of Weight 2, Dirichlet Characters, Linear Algebra, and General Modular Symbols and explain how to use linear algebra techniques to compute cusp forms and eigenforms using modular symbols.
We first discuss in Section Dirichlet Character Decomposition how to decompose
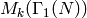 as a direct sum of subspaces corresponding to
Dirichlet characters. Next in Section Atkin-Lehner-Li Theory we state the main
theorems of Atkin-Lehner-Li theory, which
decomposes
as a direct sum of subspaces corresponding to
Dirichlet characters. Next in Section Atkin-Lehner-Li Theory we state the main
theorems of Atkin-Lehner-Li theory, which
decomposes 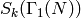 into subspaces on which the
Hecke operators act diagonalizably with “multiplicity one”.
In Section Computing Cusp Forms we describe two
algorithms for computing modular forms. One algorithm finds
a basis of
into subspaces on which the
Hecke operators act diagonalizably with “multiplicity one”.
In Section Computing Cusp Forms we describe two
algorithms for computing modular forms. One algorithm finds
a basis of 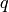 -expansions, and the other computes eigenvalues
of newforms.
-expansions, and the other computes eigenvalues
of newforms.
Dirichlet Character Decomposition¶
The group 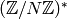 acts on
acts on 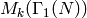 through
diamond-bracket operators
through
diamond-bracket operators 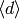 , as follows.
For
, as follows.
For 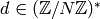 , define
, define
![f|\dbd{d} = f^{\left[\abcd{a}{b}{c}{d'}\right]_k},](_images/math/5251ec5739f742252c1dc951b32443e1029010a6.png)
where 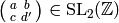 is congruent to
is congruent to
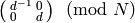 . Note that the map
. Note that the map
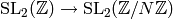 is surjective (see Exercise 1.12),
so the matrix
is surjective (see Exercise 1.12),
so the matrix 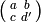 exists.
To prove that
exists.
To prove that 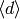 preserves
preserves 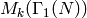 ,
we prove the more general fact that
,
we prove the more general fact that 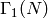 is a
normal subgroup of
is a
normal subgroup of
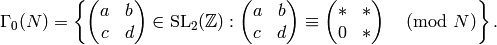
This will imply that  preserves
preserves 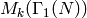 since
since 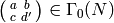 .
.
Lemma 9.1
The group 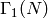 is a normal subgroup of
is a normal subgroup of 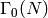 ,
and the quotient
,
and the quotient 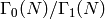 is
isomorphic to
is
isomorphic to 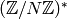 .
.
Proof
See Exercise 9.1.
Alternatively, one can prove that 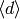 preserves
preserves
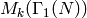 by showing that
by showing that 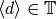 and noting that
and noting that
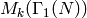 is preserved by
is preserved by 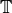 (see
Remark Remark 9.11).
(see
Remark Remark 9.11).
The diamond-bracket action is the action of
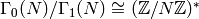 on
on 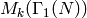 . Since
. Since
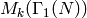 is a finite-dimensional vector space over
is a finite-dimensional vector space over 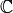 , the
, the
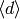 action breaks
action breaks 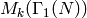 up as a direct sum of
factors corresponding to the Dirichlet characters
up as a direct sum of
factors corresponding to the Dirichlet characters 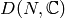 of
modulus
of
modulus  .
.
Proposition 9.2
We have
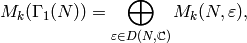
where
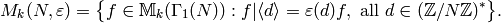
Proof
The linear transformations 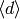 , for the
, for the 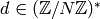 , all
commute, since
, all
commute, since 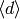 acts through the abelian group
acts through the abelian group
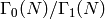 . Also, if
. Also, if  is the exponent of
is the exponent of
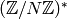 , then
, then 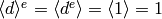 , so the
matrix of
, so the
matrix of  is diagonalizable. It is a standard fact from
linear algebra that any commuting family of diagonalizable linear
transformations is simultaneously diagonalizable (see
Exercise 5.1), so there is a basis
is diagonalizable. It is a standard fact from
linear algebra that any commuting family of diagonalizable linear
transformations is simultaneously diagonalizable (see
Exercise 5.1), so there is a basis  for
for 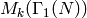 such that all
such that all 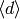 act by diagonal
matrices. The system of eigenvalues of the action of
act by diagonal
matrices. The system of eigenvalues of the action of 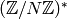 on a fixed
on a fixed
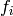 defines a Dirichlet character, i.e., each
defines a Dirichlet character, i.e., each 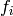 has
the property that
has
the property that 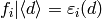 , for all
, for all
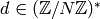 and some Dirichlet character
and some Dirichlet character 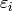 . The
. The 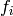 for a given
for a given  then span
then span 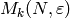 , and taken together the
, and taken together the
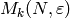 must span
must span 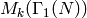 .
.
Definition 9.3
If 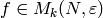 , we say that
, we say that  is
the character of the modular form
is
the character of the modular form 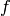 .
.
The spaces 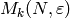 are a direct sum of subspaces
are a direct sum of subspaces
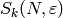 and
and 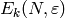 , where
, where 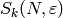 is the
subspace of cusp forms, i.e., forms that vanish at all
cusps (elements of
is the
subspace of cusp forms, i.e., forms that vanish at all
cusps (elements of 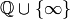 ), and
), and 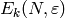 is the subspace of Eisenstein series, which is the unique
subspace of
is the subspace of Eisenstein series, which is the unique
subspace of 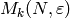 that is invariant under all Hecke
operators and is such that
that is invariant under all Hecke
operators and is such that
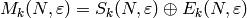 .
The space
.
The space 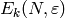 can also be defined as the space
spanned by all Eisenstein series of weight
can also be defined as the space
spanned by all Eisenstein series of weight 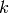 and level
and level  ,
as defined in Chapter Eisenstein Series and Bernoulli Numbers.
The space
,
as defined in Chapter Eisenstein Series and Bernoulli Numbers.
The space 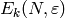 can be defined in a third way using the Petersson
inner product (see [Lan95, Section VII.5]).
can be defined in a third way using the Petersson
inner product (see [Lan95, Section VII.5]).
The diamond-bracket operators preserve cusp forms, so
the isomorphism of Proposition 9.2 restricts to an
isomorphism of the corresponding cuspidal subspaces.
We illustrate how to use Sage
to make a table of dimension of 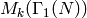 and
and 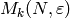 for
for 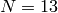 .
.
sage: G = DirichletGroup(13)
sage: G
Group of Dirichlet characters of modulus 13 over
Cyclotomic Field of order 12 and degree 4
sage: dimension_modular_forms(Gamma1(13),2)
13
sage: [dimension_modular_forms(e,2) for e in G]
[1, 0, 3, 0, 2, 0, 2, 0, 2, 0, 3, 0]
Next we do the same for 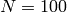 .
.
sage: G = DirichletGroup(100)
sage: G
Group of Dirichlet characters of modulus 100 over
Cyclotomic Field of order 20 and degree 8
sage: dimension_modular_forms(Gamma1(100),2)
370
sage: v = [dimension_modular_forms(e,2) for e in G]; v
[24, 0, 0, 17, 18, 0, 0, 17, 18, 0, 0, 21, 18, 0, 0, 17,
18, 0, 0, 17, 24, 0, 0, 17, 18, 0, 0, 17, 18, 0, 0, 21,
18, 0, 0, 17, 18, 0, 0, 17]
sage: sum(v)
370
Atkin-Lehner-Li Theory¶
In Section Degeneracy Maps we defined maps between modular symbols
spaces of different level. There are similar maps between spaces of
cusp forms. Suppose  and
and 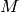 are positive integers with
are positive integers with 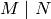 and that
and that 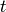 is a divisor of
is a divisor of 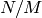 . Let
. Let
(1)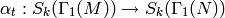
be the degeneracy map, which is given by 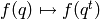 .
There are also maps
.
There are also maps 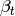 in the other direction; see
[Lan95, Ch. VIII].
in the other direction; see
[Lan95, Ch. VIII].
The old subspace of 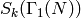 , denoted
, denoted 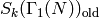 ,
is the sum of the images of all maps
,
is the sum of the images of all maps 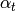 with
with 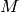 a proper divisor
of
a proper divisor
of  and
and 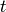 any divisor of
any divisor of 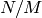 (note that
(note that 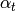 depends on
depends on
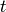 ,
,  , and
, and 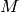 , so there is a slight abuse of notation).
The new subspace of
, so there is a slight abuse of notation).
The new subspace of 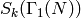 , which we denote by
, which we denote by
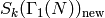 , is the intersection
of the kernel of all maps
, is the intersection
of the kernel of all maps 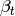 with
with  a proper divisor
of
a proper divisor
of  . One can use the Petersson inner product to show
that
. One can use the Petersson inner product to show
that
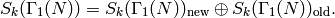
Moroever, the new and old subspaces are preserved by all Hecke operators.
Let ![\T = \Z[T_1, T_2, \ldots ]](_images/math/6a9e3fe78b30a2bace2ae1b4f66feb94fe0f9c2d.png) be the commutative polynomial ring
in infinitely many indeterminates
be the commutative polynomial ring
in infinitely many indeterminates  . This
ring acts (via
. This
ring acts (via  acting as the
acting as the 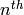 Hecke operator)
on
Hecke operator)
on 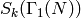 for every integer
for every integer  . Let
. Let
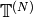 be the subring of
be the subring of 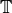 generated by the
generated by the 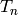 with
with
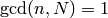 .
.
Theorem 9.4
We have a decomposition
(2)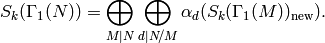
Each space 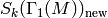 is a direct
sum of distinct (nonisomorphic) simple
is a direct
sum of distinct (nonisomorphic) simple 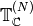 -modules.
-modules.
Proof
The complete proof is in [Li75]. See also [DS05, Ch. 5] for a beautiful modern treatement of this and related results.
The analogue of Theorem 9.4 with 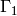 replaced by
replaced by
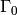 is also true (this is what was proved in
[AL70]). The analogue for
is also true (this is what was proved in
[AL70]). The analogue for 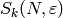 is also valid,
as long as we omit the spaces
is also valid,
as long as we omit the spaces 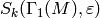 for which
for which
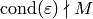 .
.
Example 9.5
If  is prime and
is prime and 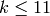 , then
, then
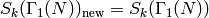 ,
since
,
since 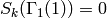 .
.
One can prove using the Petersson inner product that the
operators 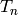 on
on 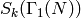 , with
, with 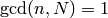 , are
diagonalizable. Another result of Atkin-Lehner-Li theory is that the
ring of endomorphisms of
, are
diagonalizable. Another result of Atkin-Lehner-Li theory is that the
ring of endomorphisms of 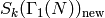 generated by all
Hecke operators equals the ring generated by the Hecke operators
generated by all
Hecke operators equals the ring generated by the Hecke operators 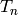 with
with 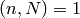 . This statement need not be true if we do not
restrict to the new subspace, as the following example shows.
. This statement need not be true if we do not
restrict to the new subspace, as the following example shows.
Example 9.6
We have
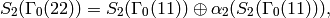
where each of the spaces 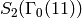 has dimension
has dimension 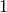 . Thus
. Thus
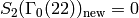 . The Hecke operator
. The Hecke operator 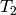 on
on
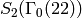 has characteristic polynomial
has characteristic polynomial 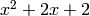 ,
which is irreducible. Since
,
which is irreducible. Since  commutes with all Hecke
operators
commutes with all Hecke
operators  , with
, with 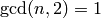 , the subring
, the subring 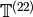 of the Hecke
algebra generated by operators
of the Hecke
algebra generated by operators 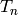 with
with 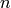 odd is isomorphic
to
odd is isomorphic
to 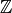 (the
(the 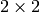 scalar matrices). Thus on the full space
scalar matrices). Thus on the full space
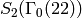 , we do not have
, we do not have 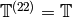 . However, on the new subspace
we do have this equality, since the new subspace has dimension
. However, on the new subspace
we do have this equality, since the new subspace has dimension 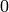 .
.
Example 9.7
The space 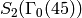 has dimension
has dimension 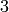 and basis
and basis
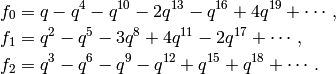
The new subspace 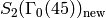 is spanned by the single cusp form
is spanned by the single cusp form
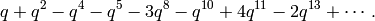
We have 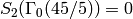 and
and 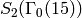 has dimension
has dimension 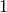 with basis
with basis
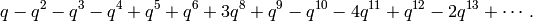
We use Sage to verify the above assertions.
sage: S = CuspForms(Gamma0(45), 2, prec=14); S
Cuspidal subspace of dimension 3 of Modular Forms space
of dimension 10 for Congruence Subgroup Gamma0(45) of
weight 2 over Rational Field
sage: S.basis()
[
q - q^4 - q^10 - 2*q^13 + O(q^14),
q^2 - q^5 - 3*q^8 + 4*q^11 + O(q^14),
q^3 - q^6 - q^9 - q^12 + O(q^14)
]
sage: S.new_subspace().basis()
(q - q^4 - q^10 - 2*q^13 + O(q^14),)
sage: CuspForms(Gamma0(9),2)
Cuspidal subspace of dimension 0 of Modular Forms space
of dimension 3 for Congruence Subgroup Gamma0(9) of
weight 2 over Rational Field
sage: CuspForms(Gamma0(15),2, prec=10).basis()
[
q - q^2 - q^3 - q^4 + q^5 + q^6 + 3*q^8 + q^9 + O(q^10)
]
Example 9.8
This example is similar to Example 9.6, except that there are newforms. We have
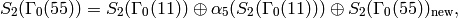
where 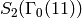 has dimension
has dimension 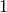 and
and
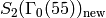 has dimension
has dimension 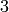 .
The Hecke operator
.
The Hecke operator 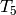 on
on
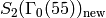 acts via the matrix
acts via the matrix
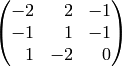
with respect to some basis.
This matrix has eigenvalues 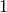 and
and 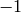 .
Atkin-Lehner theory asserts that
.
Atkin-Lehner theory asserts that 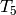 must be a
linear combination of
must be a
linear combination of 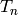 , with
, with
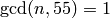 .
Upon computing the matrix for
.
Upon computing the matrix for 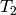 ,
we find by simple linear algebra that
,
we find by simple linear algebra that 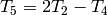 .
.
Definition 9.9
A newform is a 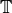 -eigenform
-eigenform 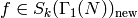 that is normalized so that the coefficient of
that is normalized so that the coefficient of 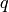 is
is 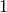 .
.
We now motivate this definition by explaining why any 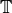 -eigenform
can be normalized so that the coefficient of
-eigenform
can be normalized so that the coefficient of 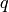 is
is 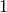 and how such
an eigenform has the property that its Fourier
coefficients are exactly the Hecke eigenvalues.
and how such
an eigenform has the property that its Fourier
coefficients are exactly the Hecke eigenvalues.
Proposition 9.10
If 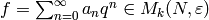 is an eigenvector for all Hecke operators
is an eigenvector for all Hecke operators
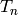 normalized so that
normalized so that 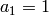 ,
then
,
then 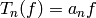 .
.
Proof
If 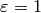 , then
, then 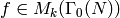 and this
is Lemma 3.22. However, we have not
yet considered Hecke operators on
and this
is Lemma 3.22. However, we have not
yet considered Hecke operators on  -expansions for
more general spaces of modular forms.
-expansions for
more general spaces of modular forms.
The Hecke operators 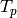 , for
, for 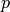 prime, act on
prime, act on 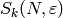 by
by
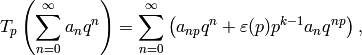
and there is a similar formula for 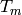 with
with 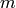 composite.
If
composite.
If 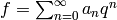 is an eigenform for all
is an eigenform for all
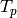 , with eigenvalues
, with eigenvalues 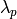 , then by the above formula
, then by the above formula
(3)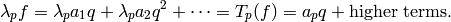
Equating coefficients of 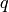 , we see that if
, we see that if
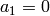 , then
, then 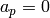 for all
for all 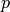 ; hence
; hence
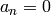 for all
for all 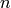 , because of the multiplicativity of Fourier
coefficients and the recurrence
, because of the multiplicativity of Fourier
coefficients and the recurrence
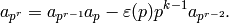
This would mean that 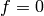 , a contradiction. Thus
, a contradiction. Thus 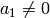 ,
and it makes sense to normalize
,
and it makes sense to normalize 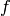 so that
so that 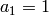 .
With this normalization, (3) implies that
.
With this normalization, (3) implies that 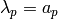 ,
as desired.
,
as desired.
Remark 9.11
The Hecke algebra 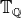 on
on 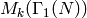 contains the
operators
contains the
operators 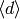 , since they satisfy the relation
, since they satisfy the relation 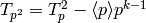 . Thus any
. Thus any  -eigenform in
-eigenform in
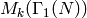 lies in a subspace
lies in a subspace 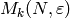 for some
Dirichlet character
for some
Dirichlet character  . Also, one can even prove that
. Also, one can even prove that
![\dbd{d} \in \Z[\ldots,T_n,\ldots]](_images/math/9dc797ae4ce7b1376dad3999d3a632b593495d6e.png) (see
Exercise 9.2).
(see
Exercise 9.2).
Computing Cusp Forms¶
Let 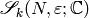 be the space of cuspidal modular symbols as in
Chapter General Modular Symbols. Let
be the space of cuspidal modular symbols as in
Chapter General Modular Symbols. Let 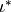 be the map of
(?), and let
be the map of
(?), and let 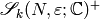 be the plus one quotient of cuspidal modular symbols,
i.e., the quotient of
be the plus one quotient of cuspidal modular symbols,
i.e., the quotient of 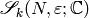 by the image of
by the image of 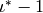 .
It follows from
Theorem 1.44 and compatibility of the
degeneracy maps (for modular symbols they are defined
in Section Degeneracy Maps) that the
.
It follows from
Theorem 1.44 and compatibility of the
degeneracy maps (for modular symbols they are defined
in Section Degeneracy Maps) that the 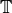 -modules
-modules 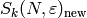 and
and 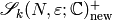 are dual as
are dual as 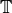 -modules.
Thus finding the systems of
-modules.
Thus finding the systems of 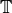 -eigenvalues on cusp forms is the same
as finding the systems of
-eigenvalues on cusp forms is the same
as finding the systems of 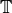 -eigenvalues on cuspidal modular
symbols.
-eigenvalues on cuspidal modular
symbols.
Our strategy to compute 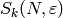 is to first compute spaces
is to first compute spaces
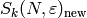 using the Atkin-Lehner-Li decomposition
(2). To compute
using the Atkin-Lehner-Li decomposition
(2). To compute 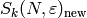 to a given
precision, we compute the systems of eigenvalues of the Hecke
operators
to a given
precision, we compute the systems of eigenvalues of the Hecke
operators 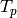 on the space
on the space 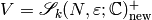 , which we
will define below. Using Proposition 9.10, we then
recover a basis of
, which we
will define below. Using Proposition 9.10, we then
recover a basis of 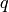 -expansions for newforms. Note that we only
need to compute Hecke eigenvalues
-expansions for newforms. Note that we only
need to compute Hecke eigenvalues 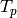 , for
, for 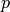 prime, not the
prime, not the 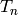 for
for 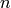 composite, since the
composite, since the 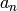 can be quickly recovered in terms
of the
can be quickly recovered in terms
of the 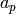 using multiplicativity and the recurrence.
using multiplicativity and the recurrence.
For some problems, e.g., construction of models for modular curves,
having a basis of 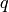 -expansions is enough. For many other problems,
e.g., enumeration of modular abelian varieties, one is really
interested in the newforms. We next discuss algorithms aimed at each
of these problems.
-expansions is enough. For many other problems,
e.g., enumeration of modular abelian varieties, one is really
interested in the newforms. We next discuss algorithms aimed at each
of these problems.
A Basis of 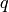 -Expansions¶
-Expansions¶
The following algorithm generalizes Algorithm 3.26.
It computes 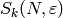 without finding any eigenspaces.
without finding any eigenspaces.
Algorithm 9.12
Given integers 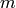 ,
,  and
and 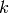 and a Dirichlet character
and a Dirichlet character  with
modulus
with
modulus  , this algorithm computes a basis of
, this algorithm computes a basis of 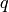 -expansions
for
-expansions
for 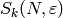 to precision
to precision 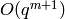 .
.
[Compute Modular Symbols] Use Algorithm 1.59 to compute
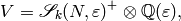
viewed as a
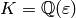 vector space,
with an action of the
vector space,
with an action of the 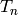 .
.[Basis for Linear Dual] Write down a basis for
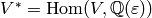 . E.g., if we identify
. E.g., if we identify
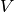 with
with 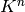 viewed as column vectors, then
viewed as column vectors, then 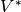 is the space
of row vectors of length
is the space
of row vectors of length 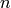 , and the pairing is the row
, and the pairing is the row 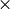 column product.
column product.[Find Generator] Find
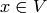 such that
such that
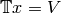 by choosing random
by choosing random 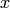 until we find
one that generates. The set of
until we find
one that generates. The set of 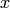 that fail
to generate lie in a union of a finite number of
proper subspaces.
that fail
to generate lie in a union of a finite number of
proper subspaces.[Compute Basis] The set of power series
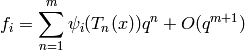
forms a basis for
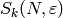 to precision
to precision  .
.
In practice Algorithm 9.12 seems slower than the
eigenspace algorithm that we will describe in the rest of this
chapter. The theoretical complexity of Algorithm 9.12
may be better, because it is not necessary to factor any
polynomials. Polynomial factorization is difficult from the worst-case
complexity point of view, though it is usually fast in practice. The
eigenvalue algorithm only requires computing a few images  for
for
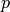 prime and
prime and 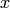 a Manin symbol on which
a Manin symbol on which 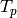 can easily be
computed. The Merel algorithm involves computing
can easily be
computed. The Merel algorithm involves computing 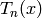 for
all
for
all 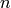 and for a fairly easy
and for a fairly easy 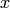 , which is potentially more work.
, which is potentially more work.
Remark 9.13
By “easy 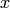 “, I mean that computing
“, I mean that computing 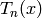 is easier on
is easier on 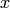 than on a completely random element of
than on a completely random element of 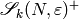 ,
e.g.,
,
e.g., 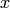 could be a Manin symbol.
could be a Manin symbol.
Newforms: Systems of Eigenvalues¶
In this section we describe an algorithm for computing the system of Hecke eigenvalues associated to a simple subspace of a space of modular symbols. This algorithm is better than doing linear algebra directly over the number field generated by the eigenvalues. It only involves linear algebra over the base field and also yields a compact representation for the answer, which is better than writing the eigenvalues in terms of a power basis for a number field. In order to use this algorithm, it is necessary to decompose the space of cuspidal modular symbols as a direct sum of simples, e.g., using Algorithm 7.17.
Fix  and a Dirichlet character
and a Dirichlet character  of modulus
of modulus  ,
and let
,
and let
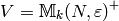
be the 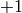 quotient of
modular symbols (see equation (?)).
quotient of
modular symbols (see equation (?)).
Algorithm 9.14
Given a 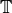 -simple subspace
-simple subspace 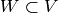 of modular symbols, this
algorithm outputs maps
of modular symbols, this
algorithm outputs maps 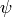 and
and  , where
, where 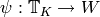 is a
is a 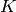 -linear map and
-linear map and 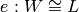 is an isomorphism of
is an isomorphism of 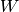 with
a number field
with
a number field 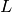 , such that
, such that 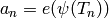 is the
eigenvalue of the
is the
eigenvalue of the 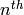 Hecke operator acting on a fixed
Hecke operator acting on a fixed
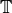 -eigenvector in
-eigenvector in 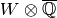 . (Thus
. (Thus
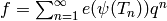 is a newform.)
is a newform.)
[Compute Projection] Let
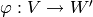 be any surjective linear map
such that
be any surjective linear map
such that 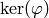 equals the kernel
of the
equals the kernel
of the 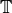 -invariant projection onto
-invariant projection onto 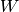 .
For example, compute
.
For example, compute 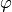 by finding a simple submodule
of
by finding a simple submodule
of 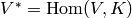 that is isomorphic to
that is isomorphic to 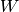 , e.g., by applying
Algorithm 7.17 to
, e.g., by applying
Algorithm 7.17 to 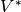 with
with 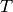 replaced by
the transpose of
replaced by
the transpose of 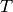 .
.[Choose
 ]label{step:eig:v} Choose a nonzero element
]label{step:eig:v} Choose a nonzero element
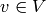 such that
such that 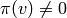 and computation of
and computation of 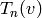 is
“easy”, e.g., choose
is
“easy”, e.g., choose  to be a Manin symbol.
to be a Manin symbol.[Map from Hecke Ring] Let
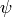 be the map
be the map 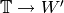 , given
by
, given
by 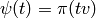 . Note that computation of
. Note that computation of 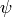 is relatively easy, because
is relatively easy, because  was chosen so that
was chosen so that
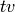 is relatively easy to compute. In particular,
if
is relatively easy to compute. In particular,
if 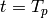 , we do not need to compute the full matrix
of
, we do not need to compute the full matrix
of 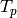 on
on 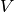 ; instead we just compute
; instead we just compute 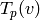 .
.[Find Generator] Find a random
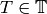 such that the iterates
such that the iterates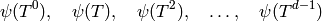
are a basis for
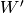 , where
, where 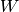 has dimension
has dimension 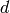 .
.[Characteristic Polynomial] Compute the characteristic polynomial
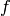 of
of 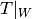 , and let
, and let ![L=K[x]/(f)](_images/math/918072d86ef54b6d9452212a795c3fddf9be60c6.png) .
Because
of how we chose
.
Because
of how we chose 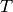 in step (4), the minimal
and characteristic polynomials of
in step (4), the minimal
and characteristic polynomials of 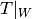 are equal, and
both are irreducible, so
are equal, and
both are irreducible, so 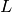 is an extension of
is an extension of 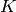 of degree
of degree 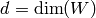 .
.[Field Structure] In this step we endow
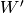 with a field structure.
Let
with a field structure.
Let 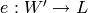 be the unique
be the unique 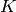 -linear isomorphism such that
-linear isomorphism such that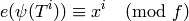
for
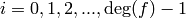 .
The map
.
The map  is uniquely determined since the
is uniquely determined since the 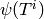 are a
basis for
are a
basis for 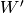 . To compute
. To compute  , we compute
the change of basis matrix from the standard basis for
, we compute
the change of basis matrix from the standard basis for 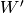 to the basis
to the basis 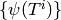 .
This change of basis matrix is the inverse
of the matrix whose rows are the
.
This change of basis matrix is the inverse
of the matrix whose rows are the 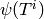 for
for 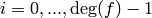 .
.[Hecke Eigenvalues] Finally for each integer
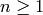 , we have
, we have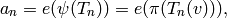
where
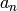 is the eigenvalue of
is the eigenvalue of 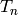 .
Output the maps
.
Output the maps 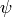 and
and  and terminate.
and terminate.
One reason we separate 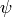 and
and  is that when
is that when 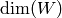 is large,
the values
is large,
the values 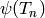 take less space to store and are easier to
compute, whereas each one of the values
take less space to store and are easier to
compute, whereas each one of the values 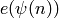 is
huge. [1] The function
is
huge. [1] The function  typically involves
large numbers if
typically involves
large numbers if 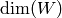 is large, since
is large, since  is obtained from the
iterates of a single vector. For many applications, e.g., databases,
it is better to store a matrix that defines
is obtained from the
iterates of a single vector. For many applications, e.g., databases,
it is better to store a matrix that defines  and the images under
and the images under
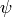 of many
of many 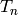 .
.
Example 9.15
The space
of cusp forms has dimension
and is spanned by two
-conjugate newforms, one of which is
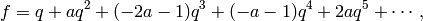
where
. We will use Algorithm 9.14 to compute a few of these coefficients.
The space
of modular symbols has dimension
. It has the following basis of Manin symbols:
![[(0,0)],\quad [(1,0)], \quad [(0,1)],](_images/math/48962b2ac25543c14b6bf281bcb52ae49b90c69f.png)
where we use square brackets to differentiate Manin symbols from vectors. The Hecke operator
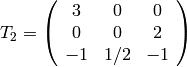
has characteristic polynomial
. The kernel of
corresponds to the span of the Eisenstein series of level
and weight
, and the kernel
of
corresponds to
. (We could also have computed
as the kernel of the boundary map
.) Each of the following steps corresponds to the step of Algorithm 9.14 with the same number.
- [Compute Projection] We compute projection onto
(this will suffice to give us a map
as in the algorithm). The matrix whose first two columns are the echelon basis for
and whose last column is the echelon basis for the Eisenstein subspace is
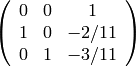
and
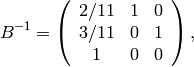
so projection onto
is given by the first two rows:
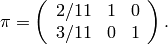
[Choose
 ] Let
] Let 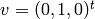 . Notice that
. Notice that 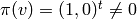 ,
and
,
and ![v=[(1,0)]](_images/math/c41bb330b44348e764d9d463c387ae21a6e31654.png) is a sum of
only one Manin symbol.
is a sum of
only one Manin symbol.[Map from Hecke Ring] This step is purely conceptual, since no actual work needs to be done. We illustrate it by computing
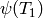 and
and 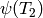 .
We have
.
We have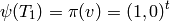
and
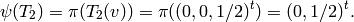
[Find Generator] We have
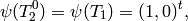
which is clearly independent from
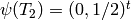 . Thus we
find that the image of the powers of
. Thus we
find that the image of the powers of 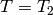 generate
generate  .
.[Characteristic Polynomial] The matrix of
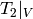 is
is 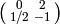 , which has characteristic
polynomial
, which has characteristic
polynomial 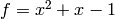 . Of course, we already knew this because
we computed
. Of course, we already knew this because
we computed 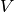 as the kernel of
as the kernel of 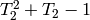 .
.[Field Structure] We have
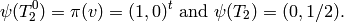
The matrix with rows the
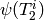 is
is 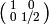 , which has inverse
, which has inverse 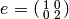 .
The matrix
.
The matrix  defines an isomorphism between
defines an isomorphism between 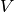 and
the field
and
the field![L=\Q[x]/(f) = \Q((-1+\sqrt{5})/2).](_images/math/31caf7df130f76e69deb412c736f0f0defbd63d6.png)
I.e.,
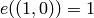 and
and 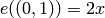 , where
, where 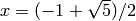 .
.[Hecke Eigenvalues] We have
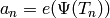 . For example,
. For example,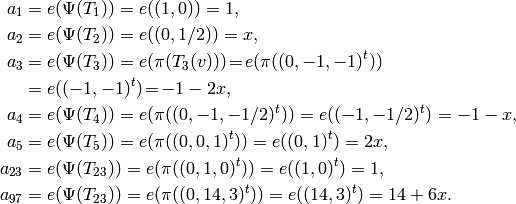
Example 9.16
It is easier to appreciate Algorithm 9.14 after seeing how big the coefficients of the power series expansion of a newform typically are, when the newform is defined over a large field. For example, there is a newform
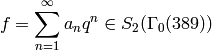
such that if 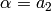 , then
, then

In contrast, if we take
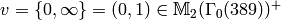 , then
, then
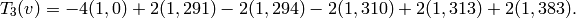
Storing 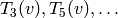 as vectors
is more compact than storing
as vectors
is more compact than storing
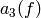 ,
, 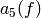 ,
,  directly as polynomials in
directly as polynomials in  !
!
Congruences between Newforms¶
This section is about congruences between modular forms. Understanding congruences is crucial for studying Serre’s conjectures, Galois representations, and explicit construction of Hecke algebras. We assume more background in algebraic number theory here than elsewhere in this book.
Congruences between Modular Forms¶
Let  be an arbitrary congruence subgroup of
be an arbitrary congruence subgroup of  ,
and suppose
,
and suppose 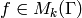 is a modular form of integer weight
is a modular form of integer weight 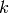 for
for 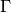 . Since
. Since 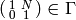 for some integer
for some integer  ,
the form
,
the form 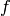 has a Fourier expansion in
nonnegative powers of
has a Fourier expansion in
nonnegative powers of 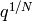 . For a rational
number
. For a rational
number 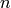 , let
, let 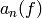 be the coefficient of
be the coefficient of 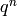 in
the Fourier expansion of
in
the Fourier expansion of 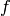 .
Put
.
Put
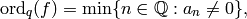
where by convention we take 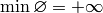 ,
so
,
so 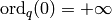 .
.
The 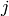 -invariant¶
-invariant¶
Let
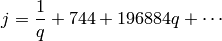
be the 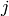 -function,
which is a weight
-function,
which is a weight 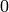 modular function
that is holomorphic except for a simple pole at
modular function
that is holomorphic except for a simple pole at 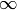 and
has integer Fourier coefficients (see, e.g.,
[Ser73, Section VIII.3.3]).
and
has integer Fourier coefficients (see, e.g.,
[Ser73, Section VIII.3.3]).
Lemma 9.17
Suppose 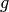 is a weight
is a weight 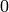 level
level 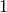 modular function that is holomorphic except possibly
with a pole of order
modular function that is holomorphic except possibly
with a pole of order 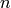 at
at 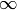 .
Then
.
Then 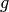 is a polynomial in
is a polynomial in 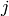 of degree at most
of degree at most 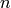 .
Moreover, the coefficients of this polynomial lie in
the ideal
.
Moreover, the coefficients of this polynomial lie in
the ideal 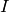 generated by the coefficients
generated by the coefficients 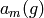 with
with 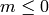 .
.
Proof
If 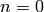 , then
, then 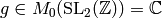 , so
, so 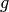 is constant with
constant term in
is constant with
constant term in 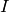 , so the statement is true. Next suppose
, so the statement is true. Next suppose 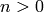 and the lemma
has been proved for all functions with smaller order poles.
Let
and the lemma
has been proved for all functions with smaller order poles.
Let 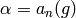 , and note that
, and note that
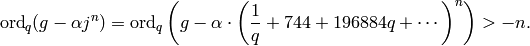
Thus by induction 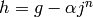 is a polynomial in
is a polynomial in 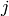 of degree
of degree 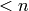 with coefficients in the ideal generated
by the coefficients
with coefficients in the ideal generated
by the coefficients 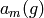 with
with 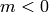 . It follows
that
. It follows
that 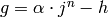 satisfies the conclusion
of the lemma.
satisfies the conclusion
of the lemma.
Sturm’s Theorem¶
If 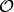 is the ring of integers of a number field,
is the ring of integers of a number field, 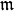 is a maximal ideal of
is a maximal ideal of 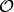 , and
, and ![f=\sum a_n q^n \in \O[[q^{1/N}]]](_images/math/d1772c706fb58c32a5305cd2c53d2c38a3233c37.png) for some integer
for some integer  ,
let
,
let
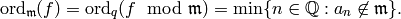
Note that 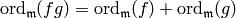 .
The following theorem was first proved in [Stu87].
.
The following theorem was first proved in [Stu87].
Theorem 9.18
Let 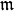 be a prime ideal in the ring of integers
be a prime ideal in the ring of integers 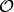 of a
number field
of a
number field 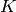 , and let
, and let 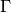 be a congruence subgroup
of
be a congruence subgroup
of 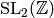 of index
of index 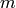 and level
and level  .
Suppose
.
Suppose 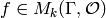 is a modular form
and
is a modular form
and
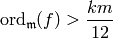
or 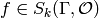 is a cusp form
and
is a cusp form
and
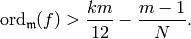
Then 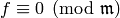 .
.
Proof
Case 1: First we assume 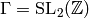 .
Let
.
Let
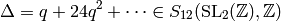
be the 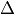 function.
Since
function.
Since 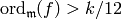 , we have
, we have 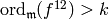 .
We have
.
We have
(4)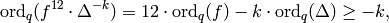
since 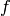 is holomorphic at infinity and
is holomorphic at infinity and 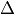 has a zero of order
has a zero of order 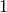 .
Also
.
Also
(5)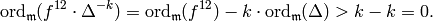
Combining (4) and (5), we see that
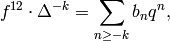
with 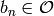 and
and 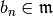 if
if 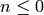 .
.
By Lemma 9.17,
![f^{12} \cdot \Delta^{-k} \in \m[j]](_images/math/2c5cb9acf6cc96636663a56034caaf38b7141bd9.png)
is a polynomial in 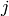 of degree at most
of degree at most 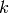 with coefficients
in
with coefficients
in 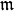 .
Thus
.
Thus
![f^{12} \in \m[j]\cdot \Delta^k,](_images/math/84ab08fa8031286209064bd97d91a23be0b2cbac.png)
so since the coefficients of 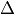 are integers, every
coefficient of
are integers, every
coefficient of 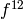 is in
is in 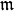 . Thus
. Thus
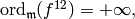 hence
hence
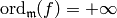 , so
, so 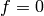 , as claimed.
, as claimed.
Case 2: 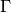 Arbitrary
Arbitrary
Let  be such that
be such that 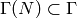 , so also
, so also
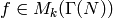 .
If
.
If 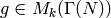 is arbitrary, then
because
is arbitrary, then
because 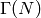 is a normal subgroup of
is a normal subgroup of 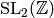 ,
we have that for any
,
we have that for any 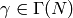 and
and 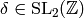 ,
,
![(g^{[\delta]_k})^{[\gamma]_k} = g^{[\delta\gamma]_k}
= g^{[\gamma'\delta]_k} = (g^{[\gamma']_k})^{[\delta]_k}
= g^{[\delta]_k},](_images/math/f9b53d468b58bcc2c4c7544b61d1ccb4187ff632.png)
where 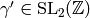 . Thus for any
. Thus for any 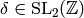 ,
we have that
,
we have that ![g^{[\delta]_k} \in M_k(\Gamma(N))](_images/math/3111279588c55172d28fcea05a0e98212418ac8e.png) , so
, so 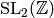 acts on
acts on 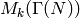 .
.
It is a standard (but nontrivial) fact about modular forms, which
comes from the geometry of the modular curve 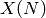 over
over 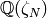 and
and ![\Z[\zeta_N]](_images/math/fd2555c28a7d149d9eae9deaf661502d6df4ba52.png) , that
, that 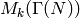 has a basis with Fourier
expansions in
has a basis with Fourier
expansions in ![\Z[\zeta_N][[q^{1/N}]]](_images/math/d734ab779d2f2afb5fb5704cfc48d04980a86909.png) and that the action of
and that the action of
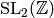 on
on 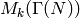 preserves
preserves
![M_k(\Gamma(N),\Q(\zeta_N)) = M_k(\Gamma(N)) \cap{}
(\Q(\zeta_N)[[q^{1/N}]])](_images/math/15021475c76cd150790d71bf6f0132258bfa06b8.png)
and the cuspidal subspace
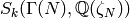 . In particular, for any
. In particular, for any
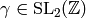 ,
,
![f^{[\gamma]_k} \in M_k(\Gamma(N), K(\zeta_N))](_images/math/9c15b73652b634318028d3d4176c0a306485eca6.png)
Moreover, the denominators of ![f^{[\gamma]_k}](_images/math/6598c12197d74870e3b7b4f310ae83d100a42400.png) are bounded, since
are bounded, since 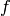 is an
is an ![\O[\zeta_N]](_images/math/8e97af206a4d40dbb5c23d7f69297cb99bf50b10.png) -linear combination of a basis for
-linear combination of a basis for
![M_k(\Gamma(N),\Z[\zeta_N])](_images/math/f08bbf8ef64d05850b33942f18614409e0201e71.png) , and the denominators of
, and the denominators of ![f^{[\gamma]_k}](_images/math/6598c12197d74870e3b7b4f310ae83d100a42400.png) divide the product of the denominators of the images of each of these
basis vectors under
divide the product of the denominators of the images of each of these
basis vectors under ![[\gamma]_k](_images/math/b982a736e025e060e88c63508ea36be04390f660.png) .
.
Let 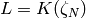 .
Let
.
Let 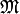 be a prime of
be a prime of 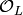 that divides
that divides
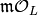 . We will now show that for each
. We will now show that for each 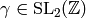 , the
Chinese Remainder Theorem implies that there is an element
, the
Chinese Remainder Theorem implies that there is an element 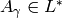 such that
such that
(6)![A_\gamma \cdot f^{[\gamma]_k} \in M_k(\Gamma(N), \O_L)
\qquad \text{and}
\qquad \ord_{\wM} (A_{\gamma} \cdot f^{[\gamma]_k}) < \infty.](_images/math/af0161390e80bf66285c5e8d02333071ec044bd0.png)
First find 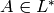 such that
such that
![A\cdot f^{[\gamma]_k}](_images/math/c06fb30ddfa5bcc9f4322119a1eb8a64ec720765.png) has coefficients in
has coefficients in 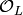 .
Choose
.
Choose 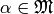 with
with 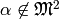 , and find a negative power
, and find a negative power
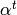 such that
such that ![\alpha^t\cdot A\cdot f^{[\gamma]_k}](_images/math/1e5d430a373980eff87f674bd3b68b5d6d8cc476.png) has
has 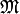 -integral coefficients and finite valuation.
This is possible because we assumed that
-integral coefficients and finite valuation.
This is possible because we assumed that 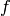 is nonzero.
Use the Chinese Remainder Theorem to find
is nonzero.
Use the Chinese Remainder Theorem to find 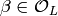 such that
such that 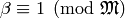 and
and 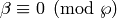 for each prime
for each prime  that divides
that divides  .
Then for some
.
Then for some  we have
we have
![\beta^s \cdot \alpha^t \cdot A\cdot f^{[\gamma]_k}
= A_\gamma \cdot f^{[\gamma]_k}
\in M_k(\Gamma(N),\O_L)](_images/math/fbd192d3c468f16ad4a892079388c9c19855e071.png)
and ![\ord_{\wM}(A_\gamma \cdot f^{[\gamma]_k}) < \infty](_images/math/89f0ef6badc3682b081f9970073ab3939cdfa99f.png) .
.
Write
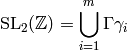
with 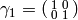 , and let
, and let
![F = f \cdot \prod_{i=2}^m A_{\gamma_i} \cdot f^{[\gamma_i]_k}.](_images/math/29b456589a08c500642bac71dceb9575cd3c0c28.png)
Then 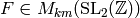 and since
and since 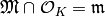 , we
have
, we
have 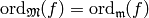 , so
, so
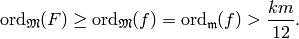
Thus we can apply Case 1 to conclude that
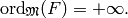
Thus
(7)![\infty = \ord_{\wM}(F) = \ord_\m(f) + \sum_{i=2}^m \ord_{\wM}(A_{\gamma_i}
f^{[\gamma]_k}),](_images/math/894af91a24f017c9b69930749dba139df238a632.png)
so 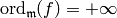 , because of (6).
, because of (6).
We next obtain a better bound when 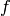 is a cusp form.
Since
is a cusp form.
Since ![[\gamma]_k](_images/math/b982a736e025e060e88c63508ea36be04390f660.png) preserves
cusp forms,
preserves
cusp forms, ![\ord_{\wM}(A_{\gamma_i} f^{[\gamma]_k}) \geq \frac{1}{N}](_images/math/554fe22c959eca073331461601d8db4efecb1c49.png) for each
for each 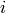 .
Thus
.
Thus
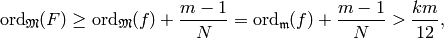
since now we are merely assuming that
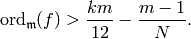
Thus we again apply Case 1 to conclude that
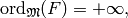 and using (7), conclude that
and using (7), conclude that
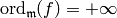 .
.
Corollary 9.19
Let 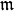 be a prime ideal in the ring of integers
be a prime ideal in the ring of integers 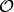 of a
number field. Suppose
of a
number field. Suppose 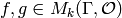 are modular
forms and
are modular
forms and
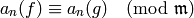
for all
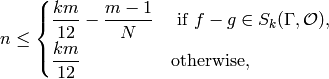
where ![m=[\SL_2(\Z):\Gamma]](_images/math/ed667d3eecfa5190d947d52146b1212979c036d9.png) .
Then
.
Then 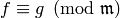 .
.
Buzzard proved the following corollary, which is extremely useful
in practical computations.
It asserts that the Sturm bound for modular forms with character
is the same as the Sturm bound for  .
.
Corollary 9.20
Let 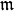 be a prime ideal in the ring of integers
be a prime ideal in the ring of integers 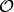 of a
number field.
Suppose
of a
number field.
Suppose 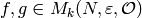 are modular
forms with Dirichlet character
are modular
forms with Dirichlet character 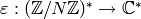 and assume
that
and assume
that
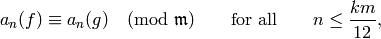
where
![m=[\SL_2(\Z):\Gamma_0(N)] =
\#\P^1(\Z/N\Z) = N \cdot \prod_{p|N}\left(1+\frac{1}{p}\right).](_images/math/e49680865e13ec6570e88b88564f1dd786d8790f.png)
Then 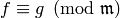 .
.
Proof
Let 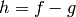 and
let
and
let 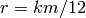 ,
so
,
so 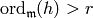 . Let
. Let  be the order of the
Dirichlet character
be the order of the
Dirichlet character  . Then
. Then 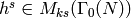 and
and
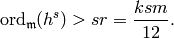
By Theorem 9.18, we have 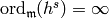 ,
so
,
so 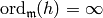 . It follows that
. It follows that 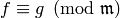 .
.
Congruence for Newforms¶
Sturm’s paper [Stu87] also applies some results of Asai on
 -expansions at various cusps to obtain a more refined result for
newforms.
-expansions at various cusps to obtain a more refined result for
newforms.
Theorem 9.21
Let  be a positive integer that is square-free, and
suppose
be a positive integer that is square-free, and
suppose 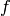 and
and 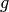 are two newforms in
are two newforms in
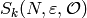 ,
where
,
where 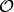 is the ring of integers of a number field,
and suppose that
is the ring of integers of a number field,
and suppose that 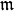 is a maximal ideal of
is a maximal ideal of 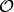 .
Let
.
Let 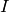 be an arbitrary subset of the prime divisors of
be an arbitrary subset of the prime divisors of  .
If
.
If 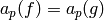 for all
for all 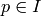 and if
and if
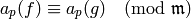
for all primes
![p \leq \frac{k\cdot [\SL_2(\Z):\Gamma_0(N)]}{12 \cdot 2^{\#I}},](_images/math/c12c977c2688bfe6507ea095381f96cc2342d3d9.png)
then 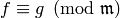 .
.
The paper [BS02] contains a similar result about
congruences between newforms, which does not require that the level be
square-free. Recall from Definition Definition 4.18 that the
conductor of a Dirichlet character  is the largest divisor
is the largest divisor  of
of  such that
such that  factors through
factors through 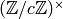 .
.
Theorem 9.22
Let  be any integer, and
suppose
be any integer, and
suppose 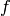 and
and 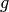 are two normalized eigenforms in
are two normalized eigenforms in 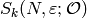 ,
where
,
where 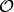 is the ring of integers of a number field,
and suppose that
is the ring of integers of a number field,
and suppose that 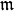 is a maximal ideal of
is a maximal ideal of 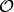 .
Let
.
Let 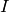 be the set of prime divisors of
be the set of prime divisors of  that
do not divide
that
do not divide 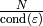 .
If
.
If
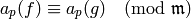
for all primes 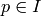 and for all primes
and for all primes
![p \leq \frac{k\cdot [\SL_2(\Z):\Gamma_0(N)]}{12 \cdot 2^{\#I}},](_images/math/c12c977c2688bfe6507ea095381f96cc2342d3d9.png)
then 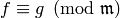 .
.
For the proof, see Lemma 1.4 and Corollary 1.7 in [BS02, Section 1.3].
Generating the Hecke Algebra¶
The following theorem appeared in [LS02, Appendix], except that
we give a better bound here. It is a nice application of the
congruence result above, which makes possible explicit computations
with Hecke rings  .
.
Theorem 9.23
Suppose 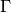 is a congruence subgroup that contains
is a congruence subgroup that contains
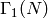 and let
and let
(8)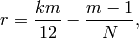
where ![m=[\SL_2(\Z):\Gamma]](_images/math/ed667d3eecfa5190d947d52146b1212979c036d9.png) .
Then the Hecke algebra
.
Then the Hecke algebra
![\T=\Z[\ldots, T_n,\ldots] \subset \End(S_k(\Gamma))](_images/math/773b46e304024d8dbdf1477ce4fd6b1b5183d520.png)
is generated as a 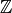 -module by the Hecke operators
-module by the Hecke operators
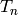 for
for 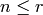 .
.
Proof
For any ring 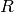 , let
, let 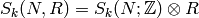 , where
, where
![S_k(N;\Z)\subset \Z[[q]]](_images/math/51f1ec56f3a0cbbeb534a89ff9c4a351d5e14ae1.png) is the submodule of cusp forms with
integer Fourier expansion at the cusp
is the submodule of cusp forms with
integer Fourier expansion at the cusp  , and let
, and let 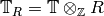 . For any ring
. For any ring  , there is a perfect pairing
, there is a perfect pairing
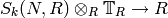
given by 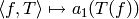 (this is true
for
(this is true
for  , hence for any
, hence for any  ).
).
Let  be the submodule of
be the submodule of  generated by
generated by
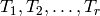 , where
, where  is the largest integer
is the largest integer
![\leq {\frac{kN}{12}}\cdot [\SL_2(\Z):\Gamma]](_images/math/52e72467050498603011d1e133dfa45ff21c58a4.png) .
Consider the exact sequence of additive abelian groups
.
Consider the exact sequence of additive abelian groups
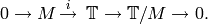
Let 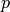 be a prime and use the fact that
tensor product is right exact to obtain an exact sequence
be a prime and use the fact that
tensor product is right exact to obtain an exact sequence
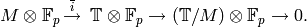
Suppose that 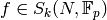 pairs to
pairs to 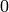 with each of
with each of
 . Then
. Then
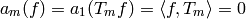
in 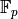 for each
for each 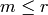 . By Theorem 9.18, it
follows that
. By Theorem 9.18, it
follows that 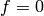 . Thus the pairing restricted to the image of
. Thus the pairing restricted to the image of
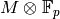 in
in 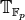 is nondegenerate, so
because (8) is perfect, it follows that
is nondegenerate, so
because (8) is perfect, it follows that
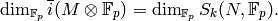
Thus 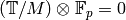 .
Repeating the argument for all primes
.
Repeating the argument for all primes 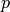 shows that
shows that 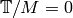 ,
as claimed.
,
as claimed.
Remark 9.24
In general, the conclusion of
Theorem 9.23 is not true if one considers only
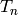 where
where 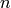 runs over the primes less than the bound.
Consider, for example,
runs over the primes less than the bound.
Consider, for example, 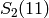 , where the bound is
, where the bound is 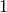 and
there are no primes
and
there are no primes 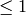 .
However, the Hecke algebra is generated as an algebra
by operators
.
However, the Hecke algebra is generated as an algebra
by operators 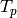 with
with 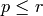 .
.
Exercises¶
Exercise 9.1
Prove that the group 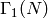 is a normal subgroup of
is a normal subgroup of
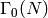 and that the quotient
and that the quotient 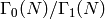 is
isomorphic to
is
isomorphic to 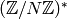 .
.
Exercise 9.2
Prove that the operators 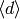 are elements of
are elements of
![\Z[\ldots,T_n,\ldots]](_images/math/720b4867a6081836c716cd0c519d9c2148da5f20.png) . [Hint: Use Dirichlet’s theorem on primes in
arithmetic progression.]
. [Hint: Use Dirichlet’s theorem on primes in
arithmetic progression.]
Exercise 9.3
Find an example like Example 9.6 but in which the new subspace
is nonzero. More precisely, find an integer  such that the Hecke
ring on
such that the Hecke
ring on 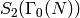 is not equal to the ring generated by
Hecke operators
is not equal to the ring generated by
Hecke operators 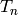 with
with 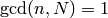 and
and
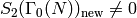 .
.
Exercise 9.4
- Following Example 9.15, compute a basis for
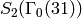 .
. - Use Algorithm 9.12 to compute a basis for
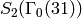 .
.
Footnotes
| [1] | John Cremona initially suggested to me the idea of separating these two maps. |